Publications

	Lightning-fast Method of Fundamental Solutions Jiong Chen, Florian Schäfer, and Mathieu Desbrun ACM Trans. Graph. 43, 4, Article 77 (SIGGRAPH), 2024. Abstract: The method of fundamental solutions (MFS) and its associated boundary element method (BEM) have gained popularity in computer graphics due to the reduced dimensionality they offer: for three-dimensional linear problems, they only require variables on the domain boundary to solve and evaluate the solution throughout space, making them a valuable tool in a wide variety of applications. However, MFS and BEM have poor computational scalability and huge memory requirements for large-scale problems, limiting their applicability and efficiency in practice. By leveraging connections with Gaussian Processes and exploiting the sparse structure of the inverses of boundary integral matrices, we introduce a variational preconditioner that can be computed via a sparse inverse-Cholesky factorization in a massively parallel manner. We show that applying our preconditioner to the Preconditioned Conjugate Gradient algorithm greatly improves the efficiency of MFS or BEM solves, up to four orders of magnitude in our series of tests.
	Stochastic Computation of Barycentric Coordinates Fernando de Goes and Mathieu Desbrun ACM Trans. Graph. 43, 4, Article 42 (SIGGRAPH), 2024. See also the accompanying video. Abstract: This paper presents a practical and general approach for computing barycentric coordinates through stochastic sampling. Our key insight is a reformulation of the kernel integral defining barycentric coordinates into a weighted least-squares minimization that enables Monte Carlo integration without sacrificing linear precision. Our method can thus compute barycentric coordinates directly at the points of interest, both inside and outside the cage, using just proximity queries to the cage such as closest points and ray intersections. As a result, we can evaluate barycentric coordinates for a large variety of cage representations (from quadrangulated surface meshes to parametric curves) seamlessly, bypassing any volumetric discretization or custom solves. To address the archetypal noise induced by sample-based estimates, we also introduce a denoising scheme tailored to barycentric coordinates. We demonstrate the efficiency and flexibility of our formulation by implementing a stochastic generation of harmonic coordinates, mean-value coordinates, and positive mean-value coordinates.
	Kinetic Simulation of Turbulent Multifluid Flows Wei Li, Kui Wu, and Mathieu Desbrun ACM Trans. Graph. 43, 4, Article 55 (SIGGRAPH), 2024. See also the accompanying video. Abstract: Despite its visual appeal, the simulation of separated multiphase flows (i.e., streams of fluids separated by interfaces) faces numerous challenges in accurately reproducing complex behaviors such as guggling, wetting, or bubbling. These difficulties are especially pronounced for high Reynolds numbers and large density variations between fluids, most likely explaining why they have received comparatively little attention in Computer Graphics compared to single- or two-phase flows. In this paper, we present a full LBM solver for multifluid simulation. We derive a conservative phase field model with which the spatial presence of each fluid or phase is encoded to allow for the simulation of miscible, immiscible and even partially-miscible fluids, while the temporal evolution of the phases is performed using a D3Q7 lattice-Boltzmann discretization. The velocity field, handled through the recent high-order moment-encoded LBM (HOME-LBM) framework to minimize its memory footprint, is simulated via a velocity-based distribution stored on a D3Q27 or D3Q19 discretization to offer accuracy and stability to large density ratios even in turbulent scenarios, while coupling with the phases through pressure, viscosity, and interfacial forces is achieved by leveraging the diffuse encoding of interfaces. The resulting solver addresses a number of limitations of kinetic methods in both computational fluid dynamics and computer graphics: it offers a fast, accurate, and low-memory fluid solver enabling efficient turbulent multiphase simulations free of the typical oscillatory pressure behavior near boundaries. We present several numerical benchmarks, examples and comparisons of multiphase flows to demonstrate our solver's visual complexity, accuracy, and realism.
	PoNQ: a Neural QEM-based Mesh Representation Nissim Maruani, Maks Ovsjanikov, Pierre Alliez, and Mathieu Desbrun CVPR, 2024. See also the project page, the accompanying video, the Supplementary Material, code, or data. Abstract: Although polygon meshes have been a standard rep resentation in geometry processing, their irregular and combinatorial nature hinders their suitability for learning based applications. In this work, we introduce a novel learnable mesh representation through a set of local 3D sample Points and their associated Normals and Quadric error metrics (QEM) w.r.t. the underlying shape, which we denote PoNQ. A global mesh is directly derived from PoNQ by efficiently leveraging the knowledge of the local quadric errors. Besides marking the first use of QEM within a neu ral shape representation, our contribution guarantees both topological and geometrical properties by ensuring that a PoNQ mesh does not self-intersect and is always the bound ary of a volume. Notably, our representation does not rely on a regular grid, is supervised directly by the target sur face alone, and also handles open surfaces with boundaries and/or sharp features. We demonstrate the efficacy of PoNQ through a learning-based mesh prediction from SDF grids and show that our method surpasses recent state-of-the-art techniques in terms of both surface and edge-based metrics.
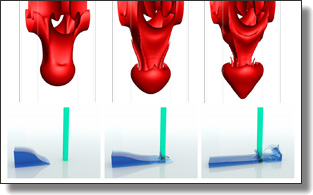	Hybrid LBM-FVM Solver for Two-phase Flow Simulation Yihui Ma, Xiaoyu Xiao, Wei Li, Mathieu Desbrun, and Xiaopei Liu Journal of Computational Science, pp. 112920, 2024. Abstract: In this paper, we introduce a hybrid LBM-FVM solver for two-phase fluid flow simulations in which interface dynamics is modeled by a conservative phase-field equation. Integrating fluid equations over time is achieved through a velocity-based lattice Boltzmann solver which is improved by a central-moment multiple-relaxation-time collision model to reach higher accuracy. For interface evolution, we propose a finite-volume-based numerical treatment for the integration of the phase-field equation: we show that the second-order isotropic centered stencils for diffusive and separation fluxes combined with the WENO-5 stencils for advective fluxes achieve similar and sometimes even higher accuracy than the state-of-the-art double-distribution function LBM methods as well as the DUGKS-based method, while requiring less computations and a smaller amount of memory. Benchmark tests (such as the 2D diagonal translation of a circular interface), along with quantitative evaluations on more complex tests (such as the rising bubble and Rayleigh-Taylor instability simulations) allowing comparisons with prior numerical methods and/or experimental data, are presented to validate the advantage of our hybrid solver. Moreover, 3D simulations (including a dam break simulation) are also compared to the time-lapse photography of physical experiments in order to allow for more qualitative evaluations.
	High-Order Moment-Encoded Kinetic Simulation of Turbulent Flows Wei Li, Tongtong Wang, Zherong Pang, Xifeng Gao, Kui Wu, and Mathieu Desbrun ACM Trans. Graph. (SIGGRAPH Asia), 42(6), 2023. See also its accompanying video. Abstract: Kinetic solvers for incompressible fluid simulation were designed to run efficiently on massively parallel architectures such as GPUs. While these lattice Boltzmann solvers have recently proven much faster and more accurate than the macroscopic Navier-Stokes-based solvers traditionally used in graphics, it systematically comes at the price of a very large memory requirement: a mesoscopic discretization of statistical mechanics requires over an order of magnitude more variables per grid node than most fluid solvers in graphics. In order to open up kinetic simulation to gaming and simulation software packages on commodity hardware, we propose a High-Order Moment-Encoded Lattice-Boltzmann-Method solver which we coined HOME-LBM, requiring only the storage of a few moments per grid node, with little to no loss of accuracy in the typical simulation scenarios encountered in graphics. We show that our lightweight and lightspeed fluid solver requires three times less memory and runs ten times faster than state-of-the-art kinetic solvers, for a nearly-identical visual output.
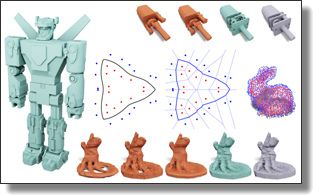	VoroMesh: Learning Watertight Surface Meshes with Voronoi Diagrams Nissim Maruani, Roman, Koklov, Maks Ovsjanikov, Pierre Alliez, and Mathieu Desbrun International Conference on Computer Vision 2023. See also its accompanying Supplementary Material, video and code, or checkout the project page for more info. Abstract: In stark contrast to the case of images, finding a concise, learnable discrete representation of 3D surfaces remains a challenge. In particular, while polygon meshes are arguably the most common surface representation used in geometry processing, their irregular and combinatorial structure often make them unsuitable for learning-based applications. In this work, we present VoroMesh, a novel and differentiable Voronoi-based representation of watertight 3D shape surfaces. From a set of 3D points (called generators) and their associated occupancy, we define our boundary representation through the Voronoi diagram of the generators as the subset of Voronoi faces whose two associated (equidistant) generators are of opposite occupancy: the resulting polygon mesh forms a watertight approximation of the target shape's boundary. To learn the position of the generators, we propose a novel loss function, dubbed VoroLoss, that minimizes the distance from ground truth surface samples to the closest faces of the Voronoi diagram which does not require an explicit construction of the entire Voronoi diagram. A direct optimization of the Voroloss to obtain generators on the Thingi32 dataset demonstrates the geometric efficiency of our representation compared to axiomatic meshing algorithms and recent learning-based mesh representations. We further use VoroMesh in a learning-based mesh prediction task from input SDF grids on the ABC dataset, and show comparable performance to state-of-the-art methods while guaranteeing closed output surfaces free of self-intersections.
	Fluid-Solid Coupling in Kinetic Two-Phase Flow Simulation Wei Li, and Mathieu Desbrun ACM Trans. Graph. (SIGGRAPH), 42(4), 2023. See also its accompanying video. Abstract: Real-life flows exhibit complex and visually appealing behaviors such as bubbling, splashing, glugging and wetting that simulation techniques in graphics have attempted to capture for years. While early approaches were not capable of reproducing multiphase flow phenomena due to their ex- cessive numerical viscosity and low accuracy, kinetic solvers based on the lattice Boltzmann method have recently demonstrated the ability to simulate water-air interaction at high Reynolds numbers in a massively-parallel fashion. However, robust and accurate handling of fluid-solid coupling has remained elusive: be it for CG or CFD solvers, as soon as the motion of immersed objects is too fast or too sudden, pressures near boundaries and interfacial forces exhibit spurious oscillations leading to blowups. Built upon a phase-field and velocity-distribution based lattice-Boltzmann solver for multiphase flows, this paper spells out a series of numerical improvements in momentum exchange, interfacial forces, and two-way coupling to drastically reduce these typical artifacts, thus significantly expanding the types of fluid-solid coupling that we can efficiently simulate. We highlight the numerical benefits of our solver through various challenging simulation results, including comparisons to previous work and real footage.
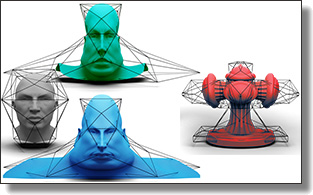	Somigliana Coordinates: an elasticity-derived approach for cage deformation Jiong Chen, Fernando de Goes, and Mathieu Desbrun ACM SIGGRAPH conference, 2023. See also its accompanying its supplemental material. Abstract: In this paper, we present a novel cage deformer based on elasticity-derived matrix-valued coordinates. In order to bypass the typical shearing artifacts and lack of volume control of existing cage deformers, we promote a more elastic behavior of the cage deformation by deriving our coordinates from the Somigliana identity, a boundary integral formulation based on the fundamental solution of linear elasticity. Given an initial cage and its deformed pose, the deformation of the cage interior is deduced from these Somigliana coordinates via a corotational scheme, resulting in a matrix-weighted combi- nation of both vertex positions and face normals of the cage. Our deformer thus generalizes Green coordinates, while producing physically-plausible spatial deformations that are invariant under similarity transformations and with interactive bulging control. We demonstrate the efficiency and versatility of our method through a series of examples in 2D and 3D.
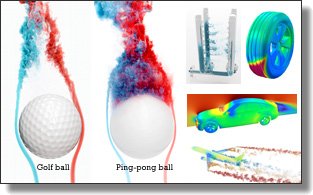	Building a Virtual Weakly-Compressible Wind Tunnel Testing Facility Chaoyang Lyu, Kai Bai, Yiheng Wu, Mathieu Desbrun, Changxi Zheng, and Xiaopei Liu ACM Trans. Graph. (SIGGRAPH), 42(4), 2023. See also its accompanying video, and its supplemental material. Abstract: Virtual wind tunnel testing is a key ingredient in the engineering design process for the automotive and aeronautical industries as well as for urban planning: through visualization and analysis of the simulation data, it helps optimize lift and drag coefficients, increase peak speed, detect high pressure zones, and reduce wind noise at low cost prior to manufacturing. In this paper, we develop an efficient and accurate virtual wind tunnel system based on recent contributions from both computer graphics and computational fluid dynamics in high-performance kinetic solvers. Running on one or multiple GPUs, our massively-parallel lattice Boltzmann model meets industry standards for accuracy and consistency while exceeding current mainstream industrial solutions in terms of efficiency Ð especially for unsteady turbulent flow simulation at very high Reynolds number (on the order of 10^7) -- due to key contributions in improved collision modeling and boundary treatment, automatic construction of multiresolution grids for complex models, as well as performance optimization. We demonstrate the efficacy and reliability of our virtual wind tunnel testing facility through comparisons of our results to multiple benchmark tests, showing an increase in both accuracy and efficiency compared to state-of-the-art industrial solutions. We also illustrate the fine turbulence structures that our system can capture, indicating the relevance of our solver for both VFX and industrial product design.
	Robust Pointset Denoising of Piecewise-Smooth Surfaces through Line Processes Jiayi Wei, Jiong Chen, Damien Rohmer, Pooran Memari, and Mathieu Desbrun Computer Graphics Forum, 42(2), 2023. Abstract: Denoising is a common, yet critical operation in geometry processing aiming at recovering high-fidelity models of piecewisesmooth objects from noise-corrupted pointsets. Despite a sizable literature on the topic, there is a dearth of approaches capable of processing very noisy and outlier-ridden input pointsets for which no normal estimates and no assumptions on the underlying geometric features or noise type are provided. In this paper, we propose a new robust-statistics approach to denoising pointsets based on line processes to offer robustness to noise and outliers while preserving sharp features possibly present in the data. While the use of robust statistics in denoising is hardly new, most approaches rely on prescribed filtering using data-independent blending expressions based on the spatial and normal closeness of samples. Instead, our approach deduces a geometric denoising strategy through robust and regularized tangent plane fitting of the initial pointset, obtained numerically via alternating minimizations for efficiency and reliability. Key to our variational approach is the use of line processes to identify inliers vs. outliers, as well as the presence of sharp features. We demonstrate that our method can denoise sampled piecewise-smooth surfaces for levels of noise and outliers at which previous works fall short.
	Efficient Kinetic Simulation of Two-Phase Flows Wei Li, Yihui Ma, Xiaopei Liu and Mathieu Desbrun ACM Trans. Graph. (SIGGRAPH), 41(4), Art. 114, 2022. See also its accompanying video, and its supplemental material. . Abstract: Real-life multiphase flows exhibit a number of complex and visually appealing behaviors, involving bubbling, wetting, splashing, and glugging. However, most state-of-the-art simulation techniques in graphics can only demonstrate a limited range of multiphase flow phenomena, due to their inability to handle the real water-air density ratio and to the large amount of numerical viscosity introduced in the flow simulation and its coupling with the interface. Recently, kinetic-based methods have achieved success in simulating large density ratios and high Reynolds numbers efficiently; but their memory overhead, limited stability, and numerically-intensive treatment of coupling with immersed solids remain enduring obstacles to their adoption in movie productions. In this paper, we propose a new kinetic solver to couple the incompressible Navier-Stokes equations with a conservative phase-field equation which remedies these major practical hurdles. The resulting two-phase immiscible fluid solver is shown to be efficient due to its massively-parallel nature and GPU implementation, as well as very versatile and reliable because of its enhanced stability to large density ratios, high Reynolds numbers, and complex solid boundaries. We highlight the advantages of our solver through various challenging simulation results that capture intricate and turbulent air-water interaction, including comparisons to previous work and real footage.
	Go Green: General Regularized Green’s Functions for Elasticity Jiong Chen and Mathieu Desbrun SIGGRAPH conference, 2022. See also supplemental material. Abstract: The fundamental solutions (Green’s functions) of linear elasticity for an infinite and isotropic media are ubiquitous in interactive graphics applications that cannot afford the computational costs of volumetric meshing and finite-element simulation. For instance, the recent work of de Goes and James [2017] leveraged these Green’s functions to formulate sculpting tools capturing in real-time broad and physically-plausible deformations more intuitively and realistically than traditional editing brushes. In this paper, we extend this family of Green’s functions by exploiting the anisotropic behavior of general linear elastic materials, where the relationship between stress and strain in the material depends on its orientation. While this more general framework prevents the existence of analytical expressions for its fundamental solutions, we show that a finite sum of spherical harmonics can be used to decompose a Green’s function, which can be further factorized into directional, radial, and material-dependent terms. From such a decoupling, we show how to numerically derive sculpting brushes to generate anisotropic deformation and finely control their falloff profiles in real-time.
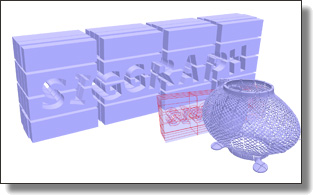	TopoCut: Fast and Robust Planar Cutting of Arbitrary Domains Xianzhong Fang, Mathieu Desbrun, Hujun Bai, and Jin Huang ACM Trans. Graph. (SIGGRAPH), 41(4), Art. 40, 2022. See also its accompanying supplemental material. Abstract: Given a complex three-dimensional domain delimited by a closed and nondegenerate input triangle mesh without any self-intersection, a common geometry processing task consists in cutting up the domain into cells through a set of planar cuts, creating a “cut-cell mesh”, i.e., a volumetric decomposition of the domain amenable to visualization (e.g., exploded views), animation (e.g., virtual surgery), or simulation (finite volume computations). A large number of methods have proposed either efficient or robust solutions, sometimes restricting the cuts to form a regular or adaptive grid for simplicity; yet, none can guarantee both properties, severely limiting their usefulness in practice. At the core of the difficulty is the determination of topological relationships among large numbers of vertices, edges, faces and cells in order to assemble a proper cut-cell mesh: while exact geometric computations provide a robust solution to this issue, their high computational cost has prompted a number of faster solutions based on, e.g., local floating-point angle sorting to significantly accelerate the process — but losing robustness in doing so. In this paper, we introduce a new approach to planar cutting of 3D domains that substitutes topological inference for numerical ordering through a novel mesh data structure, and revert to exact numerical evaluations only in the few rare cases where it is strictly necessary. We show that our novel concept of topological cuts exploits the inherent structure of cut-cell mesh generation to save computational time while still guaranteeing exactness for, and robustness to, arbitrary cuts and surface geometry. We demonstrate the superiority of our approach over state-of-the-art methods on almost 10,000 meshes with a wide range of geometric and topological complexity. We also provide an open source implementation.
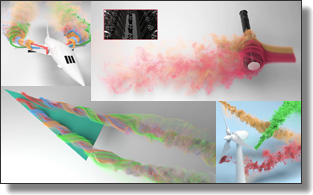	Fast and Versatile Fluid-Solid Coupling for Turbulent Flow Simulation Chaoyang Lyu, Wei Li, Mathieu Desbrun, and Xiaopei Liu ACM Trans. Graph. (SIGGRAPH), 40(6), Art. 201, 2021. See also its accompanying video. 2D code to come, please wait. Abstract: The intricate motions and complex vortical structures generated by the interaction between fluids and solids are visually fascinating. However, reproducing such a two-way coupling between thin objects and turbulent fluids numerically is notoriously challenging and computationally costly: existing approaches such as cut-cell or immersed-boundary methods have difficulty achieving physical accuracy, or even visual plausibility, of simulations involving fast-evolving flows with immersed objects of arbitrary shapes. In this paper, we propose an efficient and versatile approach for simulating two-way fluid-solid coupling within the kinetic (lattice-Boltzmann) fluid simulation framework, valid for both laminar and highly turbulent flows, and for both thick and thin objects. We introduce a novel hybrid approach to fluid-solid coupling which systematically involves a mesoscopic double-sided bounce-back scheme followed by a cut-cell velocity correction for a more robust and plausible treatment of turbulent flows near moving (thin) solids, preventing flow penetration and reducing boundary artifacts significantly. Coupled with an efficient approximation to simplify geometric computations, the whole boundary treatment method preserves the inherent massively parallel computational nature of the kinetic method. Moreover, we propose simple GPU optimizations of the core LBM algorithm which achieve an even higher computational efficiency than the state-of-the-art kinetic fluid solvers in graphics. We demonstrate the accuracy and efficacy of our two-way coupling through various challenging simulations involving a variety of rigid body solids and fluids at both high and low Reynolds numbers. Finally, comparisons to existing methods on benchmark data and real experiments further highlight the superiority of our method.
	Predicting High-Resolution Turbulence Details in Space and Time Kai Bai, Chunhao Wang, Mathieu Desbrun, and Xiaopei Liu ACM Trans. Graph. (SIGGRAPH), 40(6), Art. 200, 2021. See also its accompanying video. Code to come, please wait. Abstract: Predicting the fine and intricate details of a turbulent flow field in both space and time from a coarse input remains a major challenge despite the availability of modern machine learning tools. In this paper, we present a simple and effective dictionary-based approach to spatio-temporal upsampling of fluid simulation. We demonstrate that our neural network approach can reproduce the visual complexity of turbulent flows from spatially and temporally coarse velocity fields even when using a generic training set. Moreover, since our method generates finer spatial and/or temporal details through embarrassingly-parallel upsampling of small local patches, it can efficiently predict high-resolution turbulence details across a variety of grid resolutions. As a consequence, our method offers a whole range of applications varying from fluid flow upsampling to fluid data compression. We demonstrate the efficiency and generalizability of our method for synthesizing turbulent flows on a series of complex examples, highlighting dramatically better results in spatio-temporal upsampling and flow data compression than existing methods as assessed by both qualitative and quantitative comparisons.
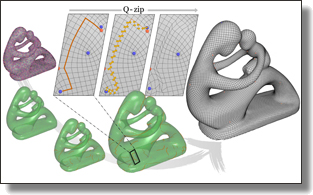	Q-zip: Singularity Editing Primitive for Quad Meshes Leman Feng, Yiying Tong, and Mathieu Desbrun ACM Trans. Graph. (SIGGRAPH), 40(6), Art. 258, 2021. Check out its accompanying supplemental material (code, meshes) too. Abstract: Singularity editing of a quadrangle mesh consists in shifting singularities around for either improving the quality of the mesh elements or canceling extraneous singularities, so as to increase mesh regularity. However, the particular structure of a quad mesh renders the exploration of allowable connectivity changes non-local and hard to automate. In this paper, we introduce a simple, principled, and general quad-mesh editing primitive with which pairs of arbitrarily distant singularities can be efficiently displaced around a mesh through a deterministic and reversible chain of local topological operations with a minimal footprint. Dubbed Q-zip as it acts as a zipper opening up and collapsing down quad strips, our practical mesh operator for singularity editing can be easily implemented via parallel transport of a reference compass between any two irregular vertices. Batches of Q-zips performed in parallel can then be used for efficient singularity editing.
	Multiscale Cholesky Preconditioning for Ill-conditioned Problems Jiong Chen, Florian Schäfer, Jin Huang, Mathieu Desbrun ACM Trans. Graph. (SIGGRAPH), 40(4), Art. 81, 2021. See also its accompanying implementation (with replicability stamp). Abstract: Many computer graphics applications boil down to solving sparse systems of linear equations. While the current arsenal of numerical solvers available in various specialized libraries and for different computer architectures often allow efficient and scalable solutions to image processing, modeling and simulation applications, an increasing number of graphics problems face large-scale and ill-conditioned sparse linear systems -- a numerical challenge which typically chokes both direct factorizations (due to high memory requirements) and iterative solvers (because of slow convergence). We propose a novel approach to the efficient preconditioning of such problems which often emerge from the discretization over unstructured meshes of partial differential equations with heterogeneous and anisotropic coefficients. Our numerical approach consists in simply performing a fine-to-coarse ordering and a multiscale sparsity pattern of the degrees of freedom, using which we apply an incomplete Cholesky factorization. By further leveraging supernodes for cache coherence, graph coloring to improve parallelism and partial diagonal shifting to remedy negative pivots, we obtain a preconditioner which, combined with a conjugate gradient solver, far exceeds the performance of existing carefully-engineered libraries for graphics problems involving bad mesh elements and/or high contrast of coefficients. We also back the core concepts behind our simple solver with theoretical foundations linking the recent method of operator-adapted wavelets used in numerical homogenization to the traditional Cholesky factorization of a matrix, providing us with a clear bridge between incomplete Cholesky factorization and multiscale analysis that we leverage numerically.
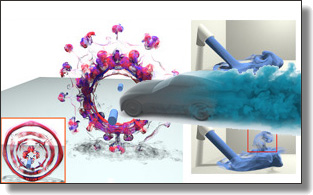	Dynamic Upsampling of Smoke through Dictionary-based Learning Kai Bai, Wei Li, Mathieu Desbrun, Xiaopei Liu ACM Trans. Graph., 40(1), Art. 4, 2020. Abstract: Simulating turbulent smoke flows with fine details is computationally intensive. For iterative editing or simply faster generation, efficiently upsampling a low-resolution numerical simulation is an attractive alternative. We propose a novel learning approach to the dynamic upsampling of smoke flows based on a training set of flows at coarse and fine resolutions. Our multiscale neural network turns an input coarse animation into a sparse linear combination of small velocity patches present in a precomputed over-complete dictionary. These sparse coefficients are then used to generate a high-resolution smoke animation sequence by blending the fine counterparts of the coarse patches. Our network is initially trained from a sequence of example simulations to both construct the dictionary of corresponding coarse and fine patches and allow for the fast evaluation of a sparse patch encoding of any coarse input. The resulting network provides an accurate upsampling when the coarse input simulation is well approximated by patches present in the training set (e.g., for re-simulation), or simply visually-plausible upsampling when input and training set differ significantly. We show a variety of examples to ascertain the strengths and limitations of our approach, and offer comparisons to existing approaches to demonstrate its quality and effectiveness.
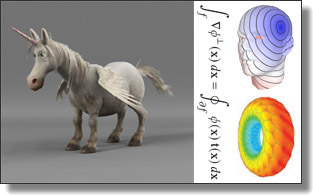	Discrete Differential Operators on Polygonal Meshes Fernando de Goes, Andrew Butts, Mathieu Desbrun ACM Trans. Graph. (SIGGRAPH), 39(4), Art. 110, 2020. Abstract: Geometry processing of surface meshes relies heavily on the discretization of differential operators such as gradient, Laplacian, and covariant derivative. While a variety of discrete operators over triangulated meshes have been developed and used for decades, a similar construction over polygonal meshes remains far less explored despite the prevalence of non-simplicial surfaces in geometric design and engineering applications. This paper introduces a principled construction of discrete differential operators on surface meshes formed by (possibly non-flat and non-convex) polygonal faces. Our approach is based on a novel mimetic discretization of the gradient operator that is linear-precise on arbitrary polygons. Equipped with this discrete gradient, we draw upon ideas from the Virtual Element Method in order to derive a series of discrete operators commonly used in graphics that are now valid over polygonal surfaces. We demonstrate the accuracy and robustness of our resulting operators through various numerical examples, before incorporating them into existing geometry processing algorithms.
	Fast and Scalable Turbulent Flow Simulation with Two-Way Coupling Wei Li, Yixin Chen, Mathieu Desbrun, Changxi Zheng, Xiaopei Liu ACM Trans. Graph. (SIGGRAPH), 39(4), Art. 47, 2020. See also its accompanying video and its supplemental material. Abstract: Despite their cinematic appeal, turbulent flows involving fluid-solid coupling remain a computational challenge in animation. At the root of this current limitation is the numerical dispersion from which most accurate Navier-Stokes solvers suffer: proper coupling between fluid and solid often generates artificial dispersion in the form of local, parasitic trains of velocity oscillations, eventually leading to numerical instability. While successive improvements over the years have led to conservative and detail-preserving fluid integrators, the dispersive nature of these solvers is rarely discussed despite its dramatic impact on fluid-structure interaction. In this paper, we introduce a novel low-dissipation and low-dispersion fluid solver that can simulate two-way coupling in an efficient and scalable manner, even for turbulent flows. In sharp contrast with most current CG approaches, we construct our solver from a kinetic formulation of the flow derived from statistical mechanics. Unlike existing lattice Boltzmann solvers, our approach leverages high-order moment relaxations as a key to controlling both dissipation and dispersion of the resulting scheme. Moreover, we combine our new fluid solver with the immersed boundary method to easily handle fluid-solid coupling through time adaptive simulations. Our kinetic solver is highly parallelizable by nature, making it ideally suited for implementation on single- or multi-GPU computing platforms. Extensive comparisons with existing solvers on synthetic tests and real-life experiments are used to highlight the multiple advantages of our work over traditional and more recent approaches, in terms of accuracy, scalability, and efficiency.
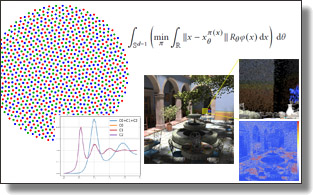	Sliced Optimal Transport Sampling Lois Paulin, Nicolas Bonneel, David Coeurjolly, Jean-Claude Iehl, Antoine Webanck, Mathieu Desbrun, Victor Ostromoukhov ACM Trans. Graph. (SIGGRAPH), 39(4), Art. 99, 2020. See also its supplemental material, as well as the project page. Abstract: In this paper, we introduce a numerical technique to generate sample distributions in arbitrary dimension for improved accuracy of Monte Carlo integration. We point out that optimal transport offers theoretical bounds on Monte Carlo integration error, and that the recently-introduced numerical framework of sliced optimal transport (SOT) allows us to formulate a novel and efficient approach to generating well-distributed high-dimensional pointsets. The resulting sliced optimal transport sampling, solely involving repeated 1D solves, is particularly simple and efficient for the common case of a uniform density over a $d$-dimensional ball. We also construct a volume-preserving map from a $d$-ball to a $d$-cube (generalizing the Shirley-Chiu mapping to arbitrary dimensions) to offer fast SOT sampling over $d$-cubes. We provide ample numerical evidence of the improvement in Monte Carlo integration accuracy that SOT sampling brings compared to existing QMC techniques, and derive a projective variant for rendering which outperforms, at times significantly, current sampling strategies using low-discrepancy sequences or optimized samples.
	Kinetic-based Multiphase Flow Simulation Wei Li, Daoming Liu, Mathieu Desbrun, Jin Huang, Xiaopei Liu IEEE Trans. Vis. Comp. Graph., 27(7), pages 3318--3334, 2021. See also its accompanying video. Abstract: Simulating turbulent smoke flows is computationally intensive due to their intrinsic multiscale behavior, thus requiring sophisticated non-dissipative solvers with relatively high resolution to fully capture their complexity. For iterative editing or simply faster generation of smoke flows, dynamic upsampling of an input low-resolution numerical simulation is an attractive, yet currently unattainable goal. In this paper, we propose a novel dictionary-based learning approach to the dynamic upsampling of smoke flows. For each frame of an input coarse animation, we seek a sparse representation of small, local velocity patches of the flow based on an over-complete dictionary, and use the resulting sparse coefficients to generate a high-resolution animation sequence. We introduce a neural network which learns both a fast evaluation of sparse patch encoding and a dictionary of corresponding coarse and fine patches from a sequence of simulations computed with any numerical solver. Because our approach amounts to learning the integration of fine Navier-Stokes flow patches from their counterparts simulated on a coarse grid, our upsampling process injects into coarse input sequences physics-driven fine details, unlike most previous approaches that only employed fast procedural models to add high frequency to the input. Our use of sparse representation also avoids excessive blurring during synthesis while retaining complex structures, thus offering increased efficiency and visual realism. Using a training set composed of local patches of the velocity field from a set of coarse and fine simulation pairs, our approach can upsample an arbitrary coarse simulation, very accurately if the training examples cover enough dynamic variety, or just plausibly otherwise. We present a variety of upsampling results for smoke flows with different training settings (generalized synthesis, restricted synthesis and re-simulation) exhibiting different synthesis quality, and offer comparisons to their corresponding high-resolution simulations to indicate the effectiveness of our approach to efficiently and realistically simulating high-resolution smoke flows.
	Laplacian-Optimized Diffusion for Semi-Supervised Learning Max Budninskiy, Ameera Abdelaziz, Yiying Tong, and Mathieu Desbrun Computer Aided Geometric Design (special issue on Geometric Modeling and Processing), 79:101864, 2020. Abstract: Semi-supervised learning (SSL) is fundamentally a geometric task: in order to classify high-dimensional point sets when only a small fraction of data points are labeled, the geometry of the unlabeled data points is exploited to gain better classifying accuracy. A number of state-of-the-art SSL techniques rely on label propagation through graph-based diffusion, with edge weights that are evaluated either analytically from the data or through compute-intensive training based on nonlinear and nonconvex optimization. In this paper, we bring discrete differential geometry to bear on this problem by introducing a graph-based SSL approach where label diffusion uses a Laplacian operator learned from the geometry of the input data. From a data-dependent graph of the input, we formulate a biconvex loss function in terms of graph edge weights and inferred labels. Its minimization is achieved through alternating rounds of optimization of the Laplacian and diffusion-based inference of labels. The resulting optimized Laplacian diffusion directionally adapts to the intrinsic geometric structure of the data which often concentrates in clusters or around low-dimensional manifolds within the high-dimensional representation space. We show on a range of classical datasets that our variational classification is more accurate than current graph-based SSL techniques. The algorithmic simplicity and efficiency of our discrete differential geometric approach (limited to basic linear algebra operations) also make it attractive, despite the seemingly complex task of optimizing all the edge weights of a graph.
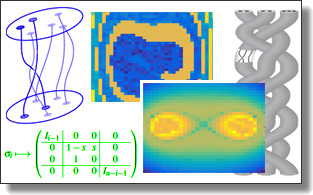	Material Coherence from Trajectories via Burau Eigenanalysis of Braids Melissa Yeung, David Cohen-Steiner, Mathieu Desbrun Chaos 30, 033122, 2020. Abstract: In this paper, we provide a numerical tool to study material coherence from a set of 2D Lagrangian trajectories sampling a dynamical system, i.e., from the motion of passive tracers. We show that eigenvectors of the Burau representation of a topological braid derived from the trajectories have levelsets corresponding to components of the Nielsen--Thurston decomposition of the dynamical system. One can thus detect and identify clusters of space-time trajectories corresponding to coherent regions of the dynamical system by solving an eigenvalue problem. Unlike previous methods, the scalable computational complexity of our braid-based approach allows the analysis of large amounts of trajectories.
	3D Hodge Decompositions of Edge- and Face-based Vector Fields Rundong Zhao, Mathieu Desbrun, Guo-Wei Wei, and Yiying Tong ACM Trans. Graph. (SIGGRAPH Asia), 38(6), Art. 181, 2019. Code available on github. Abstract: We present a compendium of Hodge decompositions of vector fields on tetrahedral meshes embedded in the 3D Euclidean space. After describing the foundations of the Hodge decomposition in the continuous setting, we describe how to implement a five-component orthogonal decomposition that generically splits, for a variety of boundary conditions, any given discrete vector field expressed as discrete differential forms into two potential fields, as well as three additional harmonic components that arise from the topology or boundary of the domain. The resulting decomposition is proper and mimetic, in the sense that the theoretical dualities on the kernel spaces of vector Laplacians valid in the continuous case (including correspondences to cohomology and homology groups) are exactly preserved in the discrete realm. Such a decomposition only involves simple linear algebra with symmetric matrices, and can thus serve as a basic computational tool for vector field analysis in graphics, electromagnetics, fluid dynamics and elasticity.
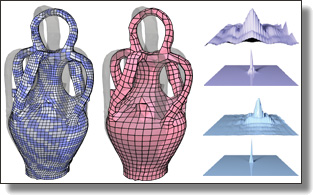	Material-adapted Refinable Basis Functions for Elasticity Simulation Jiong Chen, Max Budninskiy, Houman Owhadi, Hujun Bao, Jin Huang, and Mathieu Desbrun. ACM Trans. Graph. (SIGGRAPH Asia), 38(6), Art. 161, 2019. Abstract: In this paper, we introduce a hierarchical construction of material-adapted refinable basis functions and associated wavelets to offer efficient coarse-graining of linear elastic objects. While spectral methods rely on global basis functions to restrict the number of degrees of freedom, our basis functions are locally supported; yet, unlike typical polynomial basis functions, they are adapted to the material inhomogeneity of the elastic object to better capture its physical properties and behavior. In particular, they share spectral approximation properties with eigenfunctions, offering a good compromise between computational complexity and accuracy. Their construction involves only linear algebra and follows a fine-to-coarse approach, leading to a block-diagonalization of the stiffness matrix where each block corresponds to an intermediate scale space of the elastic object. Once this hierarchy has been precomputed, we can simulate an object at runtime on very coarse resolution grids and still capture the correct physical behavior, with orders of magnitude speedup compared to a fine simulation. We show on a variety of heterogeneous materials that our approach outperforms all previous coarse-graining methods for elasticity.
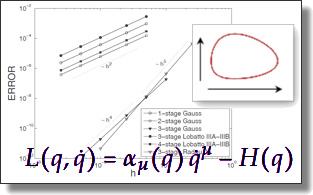	Variational partitioned Runge-Kutta methods for Lagrangians linear in velocities Tomasz M. Tyranowski and Mathieu Desbrun. Mathematics 7(9), Art. 861, 2019. Abstract: In this paper, we construct higher-order variational integrators for a class of degenerate systems described by Lagrangians that are linear in velocities. We analyze the geometry underlying such systems and develop the appropriate theory for variational integration. Our main observation is that the evolution takes place on the primary constraint and the “Hamiltonian” equations of motion can be formulated as an index-1 differential-algebraic system. We also construct variational Runge–Kutta methods and analyze their properties. The general properties of Runge–Kutta methods depend on the “velocity” part of the Lagrangian. If the “velocity” part is also linear in the position coordinate, then we show that non-partitioned variational Runge–Kutta methods are equivalent to integration of the corresponding first-order Euler–Lagrange equations, which have the form of a Poisson system with a constant structure matrix, and the classical properties of the Runge–Kutta method are retained. If the “velocity” part is nonlinear in the position coordinate, we observe a reduction of the order of convergence, which is typical of numerical integration of DAEs. We verified our results through numerical experiments for various dynamical systems.
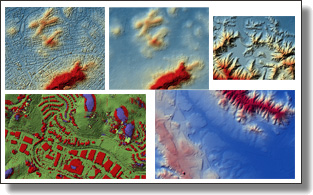	Large-scale DTM Generation from Satellite Data Liuyun Duan, Mathieu Desbrun, Anne Giraud, Frédéric Trastour, Lionel Laurore. CVPR EarthVision Workshop (IEEE/ISPRS Large Scale Computer Vision for Remote Sensing Imagery), June 2019. Abstract: In remote sensing, Digital Terrain Models (DTM) generation is a long-standing problem involving bare-terrain extraction and surface reconstruction to estimate a DTM from a Digital Surface Model (DSM). Most existing methods (including commercial software packages) have difficulty handling large-scale satellite data of inhomogeneous quality and resolution, and often need an expert-driven manual parameter-tuning process for each geographical type of DSM. In this paper we propose an automated and versatile DTM generation method from satellite data that is perfectly suited to large-scale applications. A novel set of feature descriptors based on multiscale morphological analysis are first computed to extract reliable bare-terrain elevations from DSMs. This terrain extraction algorithm is robust to noise and adapts well to local reliefs in both flat and highly mountainous areas. Then, we reconstruct the final DTM mesh using relative coordinates with respect to the sparse elevations previously detected, and induce preservation of geometric details by adapting these coordinates based on local relief attributes. Experiments on worldwide DSMs show the potential of our approach for large-scale DTM generation without parameter tuning. Our system is flexible as well, as it allows for a straightforward integration of multiple external masks (e.g., forest, road line, buildings, lake, etc) to better handle complex cases, resulting in further improvements of the quality of the output DTM.
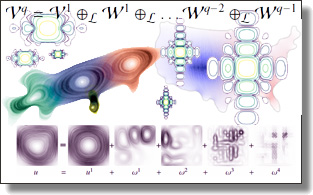	Operator-adapted wavelets for finite-element differential forms Max Budninskiy, Houman Owhadi, and Mathieu Desbrun. Journal of Computational Physics, 388, pp. 144-177, 2019. Abstract: We introduce in this paper an operator-adapted multiresolution analysis for finite-element differential forms. From a given continuous, linear, bijective, and self-adjoint positive-definite operator L, a hierarchy of basis functions and associated wavelets for discrete differential forms is constructed in a fine-tocoarse fashion and in quasilinear time. The resulting wavelets are L-orthogonal across all scales, and can be used to derive a Galerkin discretization of the operator such that its stiffness matrix becomes block-diagonal, with uniformly well-conditioned and sparse blocks. Because our approach applies to arbitrary differential p-forms, we can derive both scalar-valued and vector-valued wavelets block-diagonalizing a prescribed operator. We also discuss the generality of the construction by pointing out that it applies to various types of computational grids, offers arbitrary smoothness orders of basis functions and wavelets, and can accommodate linear differential constraints such as divergence-freeness. Finally, we demonstrate the benefits of the corresponding operator-adapted multiresolution decomposition for coarse-graining and model reduction of linear and non-linear partial differential equations.
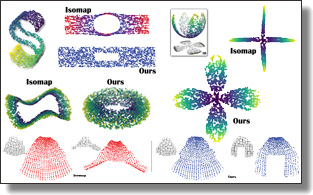	Parallel Transport Unfolding: A Connection-based Manifold Learning Approach Max Budninskiy, Gloria Yin, Leman Feng, Yiying Tong, and Mathieu Desbrun. SIAM J. Appl. Algebra Geometry, 3(2), pp. 266-291, 2019. Code base available on Github, and the notebook of all examples is here Abstract: Manifold learning offers nonlinear dimensionality reduction of high-dimensional datasets. In this paper, we bring geometry processing to bear on manifold learning by introducing a new approach based on metric connection for generating a quasi-isometric, low-dimensional mapping from a sparse and irregular sampling of an arbitrary manifold embedded in a high-dimensional space. Geodesic distances of discrete paths over the input pointset are evaluated through ``parallel transport unfolding'' (PTU) to offer robustness to poor sampling and arbitrary topology. Our new geometric procedure exhibits the same strong resilience to noise as one of the staples of manifold learning, the Isomap algorithm, as it also exploits all pairwise geodesic distances to compute a low-dimensional embedding. While Isomap is limited to geodesically-convex sampled domains, parallel transport unfolding does not suffer from this crippling limitation, resulting in an improved robustness to irregularity and voids in the sampling. Moreover, it involves only simple linear algebra, significantly improves the accuracy of all pairwise geodesic distance approximations, and has the same computational complexity as Isomap. Finally, we show that our connection-based distance estimation can be used for faster variants of Isomap such as L-Isomap.
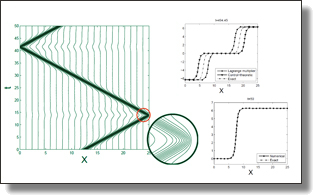	R-adaptive multisymplectic and variational integrators Tomasz M. Tyranowski and Mathieu Desbrun. Mathematics 7(7), Art. 642, 2019. Abstract: Moving mesh methods (also called r-adaptive methods) are space-adaptive strategies used for the numerical simulation of time-dependent partial differential equations. These methods keep the total number of mesh points fixed during the simulation but redistribute them over time to follow the areas where a higher mesh point density is required. There are a very limited number of moving mesh methods designed for solving field-theoretic partial differential equations, and the numerical analysis of the resulting schemes is challenging. In this paper, we present two ways to construct r-adaptive variational and multisymplectic integrators for (1+1)-dimensional Lagrangian field theories. The first method uses a variational discretization of the physical equations, and the mesh equations are then coupled in a way typical of the existing r-adaptive schemes. The second method treats the mesh points as pseudo-particles and incorporates their dynamics directly into the variational principle. A user-specified adaptation strategy is then enforced through Lagrange multipliers as a constraint on the dynamics of both the physical field and the mesh points. We discuss the advantages and limitations of our methods. Numerical results for the Sine–Gordon equation are also presented.
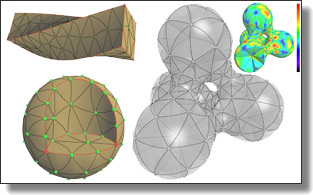	Curved Optimal Delaunay Triangulation Leman Feng, Pierre Alliez, Laurent Busé, Hervé Delingette, and Mathieu Desbrun. ACM Trans. Graph., 37(4), Art. 61, 2018. See also Supplemental Material. Abstract: Meshes with curvilinear elements hold the appealing promise of enhanced geometric flexibility and higher-order numerical accuracy compared to their commonly-used straight-edge counterparts. However, the generation of curved meshes remains a computationally expensive endeavor with current meshing approaches: high-order parametric elements are notoriously difficult to conform to a given boundary geometry, and enforcing a smooth and non-degenerate Jacobian everywhere brings additional numerical difficulties to the meshing of complex domains. In this paper, we propose an extension of Optimal Delaunay Triangulations (ODT) to curved and graded isotropic meshes. By exploiting a continuum mechanics interpretation of ODT instead of the usual approximation theoretical foundations, we formulate a very robust geometry and topology optimization of Bézier meshes based on a new simple functional promoting isotropic and uniform Jacobians throughout the domain. We demonstrate that our resulting curved meshes can adapt to complex domains with high precision even for a small count of elements thanks to the added flexibility afforded by more control points and higher order basis functions.
	Quadrangulation through Morse-Parameterization Hybridization Xianzhong Fang, Hujun Bao, Yiying Tong, Mathieu Desbrun, and Jin Huang. ACM Trans. Graph., 37(4), Art. 92, 2018. See also Supplemental Material, and Thingi10K addendum. Binary code (Linux Mint 19 Cinnamon or Ubuntu 18.04) available too. Abstract: We introduce an approach to quadrilateral meshing of arbitrary triangulated surfaces that combines the theoretical guarantees of Morse-based approaches with the practical advantages of parameterization methods. We first construct, through an eigensolver followed by a few Gauss-Newton iterations, a periodic four-dimensional vector field that aligns with a user-provided frame field and/or a set of features over the input mesh. A field-aligned parameterization is then greedily computed along a spanning tree based on the Dirichlet energy of the optimal periodic vector field, from which quad elements are efficiently extracted over most of the surface. The few regions not yet covered by elements are then upsampled and the first component of the periodic vector field is used as a Morse function to extract the remaining quadrangles. This hybrid parameterization- and Morse-based quad meshing method is not only fast (the parameterization is greedily constructed, and the Morse function only needs to be upsampled in the few uncovered patches), but is guaranteed to provide a feature-aligned quad mesh with non-degenerate cells that closely matches the input frame field over an arbitrary surface. We show that our approach is much faster than Morse-based techniques since it does not require a densely tessellated input mesh, and is significantly more robust than parameterization-based techniques on models with complex features.
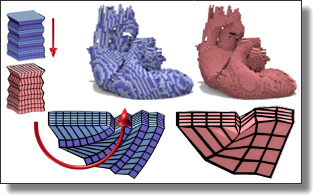	Numerical Coarsening using Discontinuous Shape Functions Jiong Chen, Hujun Bao, Tianyu Wang, Mathieu Desbrun, and Jin Huang. ACM Trans. Graph., 37(4), Art. 117, 2018. Abstract: In this paper, an efficient and scalable approach for simulating inhomogeneous and non-linear elastic objects is introduced. Our numerical coarsening approach consists in optimizing non-conforming and matrix-valued shape functions to allow for predictive simulation of heterogeneous materials with non-linear constitutive laws even on coarse grids, thus saving orders of magnitude in computational time compared to traditional finite element computations. The set of local shape functions over coarse elements is carefully tailored in a preprocessing step to balance geometric continuity and local material stiffness. In particular, we do not impose continuity of our material-aware shape functions between neighboring elements to significantly reduce the fictitious numerical stiffness that conforming bases induce; however, we enforce crucial geometric and physical properties such as partition of unity and exact reproduction of representative fine displacements to eschew the use of discontinuous Galerkin methods. We demonstrate that we can simulate, with no parameter tuning, inhomogeneous and non-linear materials significantly better than previous approaches that traditionally try to homogenize the constitutive model instead.
	LicPy Dzhelil Rufat. Standalone Python library, Github, 2018. See also https://dzhelil.info/licpy for the documentation. Abstract: LicPy is an implementation in Python of the Line Integral Convolution (LIC) method: from licpy.lic import runlic tex = runlic(vx, vy, L) grey_save(dest, tex)
	Planar Shape Detection at Structural Scales Hao Fang, Florent Lafarge, and Mathieu Desbrun. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018, pp. 2965-2973. Abstract: Interpreting 3D data such as point clouds or surface meshes depends heavily on the scale of observation. Yet, existing algorithms for shape detection rely on trial-anderror parameter tunings to output configurations representative of a structural scale. We present a framework to automatically extract a set of representations that capture the shape and structure of man-made objects at different key abstraction levels. A shape-collapsing process first generates a fine-to-coarse sequence of shape representations by exploiting local planarity. This sequence is then analyzed to identify significant geometric variations between successive representations through a supervised energy minimization. Our framework is flexible enough to learn how to detect both existing structural formalisms such as the CityGML Levels Of Details, and expert-specified levels of abstraction. Experiments on different input data and classes of manmade objects, as well as comparisons with existing shape detection methods, illustrate the strengths of our approach in terms of efficiency and flexibility.
	Spectral Affine-Kernel Embeddings Max Budninskiy, Beibei Liu, Yiying Tong, and Mathieu Desbrun. Symposium on Geometry Processing (won one of the Best Paper awards), Computer Graphics Forum, volume 36, 2017. Abstract: In this paper, we propose a controllable embedding method for high- and low-dimensional geometry processing through sparse matrix eigenanalysis. Our approach is equally suitable to perform non-linear dimensionality reduction on big data, or to offer non-linear shape editing of 3D meshes and pointsets. At the core of our approach is the construction of a multi-Laplacian quadratic form that is assembled from local operators whose kernels only contain locally-affine functions. Minimizing this quadratic form provides an embedding that best preserves all relative coordinates of points within their local neighborhoods. We demonstrate the improvements that our approach brings over existing nonlinear dimensionality reduction methods on a number of datasets, and formulate the first eigen-based as-rigid-as-possible shape deformation technique by applying our affine-kernel embedding approach to 3D data augmented with user-imposed constraints on select vertices.
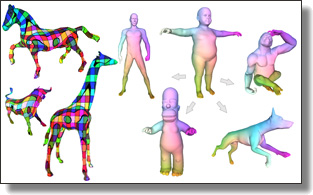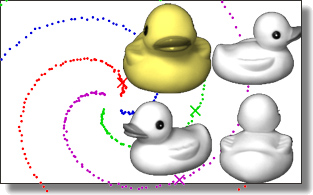
	Variance-Minimizing Transport Plans for Inter-surface Mapping Manish Mandad, David Cohen-Steiner, Leif Kobbelt, Pierre Alliez, and Mathieu Desbrun. ACM Trans. Graph., 36(4), 2017. See also Supplemental Material. Abstract: We introduce an efficient computational method for generating dense and low distortion maps between two arbitrary surfaces of same genus. Instead of relying on semantic correspondences or surface parameterization, we directly optimize a variance-minimizing transport plan between two input surfaces that defines an as-conformal-as-possible inter-surface map satisfying a user-prescribed bound on area distortion. The transport plan is computed via two alternating convex optimizations, and is shown to minimize a generalized Dirichlet energy of both the map and its inverse. Computational efficiency is achieved through a coarse-to-fine approach in diffusion geometry, with Sinkhorn iterations modified to enforce bounded area distortion. The resulting inter-surface mapping algorithm applies to arbitrary shapes robustly, with little to no user interaction.
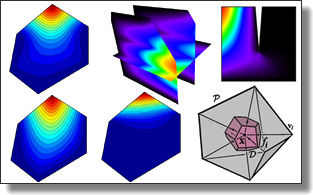	Power Coordinates: A Geometric Construction of Barycentric Coordinates on Convex Polytopes Max Budninskiy, Beibei Liu, Yiying Tong, and Mathieu Desbrun. ACM Trans. Graph., 35(6), 2016. Supplemental Material: base code. Abstract: We present a full geometric parameterization of generalized barycentric coordinates on convex polytopes. We show that these continuous and non-negative coefficients ensuring linear precision can be efficiently and exactly computed through a power diagram of the polytope's vertices and the evaluation point. In particular, we point out that well-known explicit coordinates such as Wachspress, Discrete Harmonic, Voronoi, or Mean Value correspond to simple choices of power weights. We also present examples of new barycentric coordinates, and discuss possible extensions such as power coordinates for non-convex polygons and smooth shapes.
	Optimal Voronoi Tessellations with Hessian-based Anisotropy Max Budninskiy, Beibei Liu, Fernando de Goes, Yiying Tong, Pierre Alliez, and Mathieu Desbrun. ACM Trans. Graph., 35(6), 2016. Supplemental Material. Abstract: This paper presents a variational method to generate cell complexes with local anisotropy conforming to the Hessian of any given convex function and for any given local mesh density. Our formulation builds upon approximation theory to offer an anisotropic extension of Centroidal Voronoi Tessellations which can be seen as a dual form of Optimal Delaunay Triangulation. We thus refer to the resulting anisotropic polytopal meshes as Optimal Voronoi Tessellations. Our approach sharply contrasts with previous anisotropic versions of Voronoi diagrams as it employs first-type Bregman diagrams, a generalization of power diagrams where sites are augmented with not only a scalar-valued weight but also a vectorvalued shift. As such, our OVT meshes contain only convex cells with straight edges, and admit an embedded dual triangulation that is combinatorially-regular. We show the effectiveness of our technique using off-the-shelf computational geometry libraries.
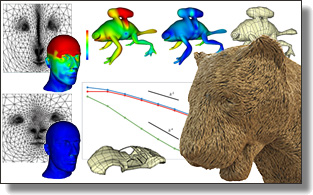	Subdivision Exterior Calculus for Geometry Processing Fernando de Goes, Mathieu Desbrun, Mark Meyer, and Tony DeRose. ACM Trans. Graph., 35(4), Art. 133, 2016. Supplemental Material part I, part II. Abstract: This paper introduces a new computational method to solve differential equations on subdivision surfaces. Our approach adapts the numerical framework of Discrete Exterior Calculus (DEC) from the polygonal to the subdivision setting by exploiting the refinability of subdivision basis functions. The resulting Subdivision Exterior Calculus (SEC) provides significant improvements in accuracy compared to existing polygonal techniques, while offering exact finite-dimensional analogs of continuum structural identities such as Stokes' theorem and Helmholtz-Hodge decomposition. We demonstrate the versatility and efficiency of SEC on common geometry processing tasks including parameterization, geodesic distance computation, and vector field design.
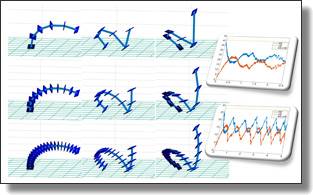	A Multisymplectic Integrator for Elastodynamic Frictionless Impact Problems François Demoures, François Gay-Balmaz, Mathieu Desbrun, Tudor S. Ratiu, and Alejandro M. Aragón. Computer Methods in Applied Mechanics and Engineering, Volume 315, p. 1025-1052, March 2017. Abstract: We present a structure preserving numerical algorithm for the collision of elastic bodies. Our integrator is derived from a discrete version of the field-theoretic (multisymplectic) variational description of nonsmooth Lagrangian continuum mechanics, combined with generalized Lagrange multipliers to handle inequality constraints. We test the resulting explicit integrator for the longitudinal impact of two elastic linear bar models, and for the collision of a nonlinear geometrically exact beam model with a rigid plane. Numerical simulations for various physical parameters are presented to illustrate the behavior and performance of our approach.
	Vector field processing on triangle meshes Fernando de Goes, Mathieu Desbrun, and Yiying Tong. Course notes, ACM SIGGRAPH 2016. (powerpoint slides available here) Abstract: While scalar fields on surfaces have been staples of geometry processing, the use of tangent vector fields has steadily grown in geometry processing over the last two decades: they are crucial to encode both directions and sizing on surfaces as commonly required in tasks such as texture synthesis, non-photorealistic rendering, digital grooming, and meshing. There are, however, a variety of discrete representations of tangent vector fields on triangle meshes, and each approach offers different trade-offs among simplicity, efficiency, and accuracy depending on the targeted application. This course reviews the three main families of discretizations used to design computational tools for vector field processing on triangle meshes: face-based, edge-based, and vertex-based representations. In the process of reviewing the computational tools offered by these representations, we go over a large body of recent developments in vector field processing in the area of discrete differential geometry. We also discuss the theoretical and practical limitations of each type of discretization, and cover increasingly-common extensions such as n-direction and n-vector fields. While the course will focus on explaining the key approaches to practical encoding (including data structures) and manipulation (including discrete operators) of finitedimensional vector fields, important differential geometric notions will also be covered: as often in Discrete Differential Geometry, the discrete picture will be used to illustrate deep continuous concepts such as covariant derivatives, metric connections, or Bochner Laplacians.
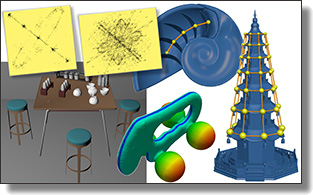	Symmetry and Orbit Detection via Lie-Algebra Voting Zeyun Shi, Pierre Alliez, Mathieu Desbrun, Hujun Bao, and Jin Huang. Symposium of Geometry Processing (won one of the Best Paper awards), CGF, 26(5):217–227, 2016. See also supplemental material, and hindsight. Abstract: In this paper, we formulate an automatic approach to the detection of partial, local, and global symmetries and orbits in arbitrary 3D datasets. We improve upon existing voting-based symmetry detection techniques by leveraging the Lie group structure of geometric transformations. In particular, we introduce a logarithmic mapping that ensures that orbits are mapped to linear subspaces, hence unifying and extending many existing mappings in a single Lie-algebra voting formulation. Compared to previous work, our resulting method offers significantly improved robustness as it guarantees that our symmetry detection of an input model is frame, scale, and reflection invariant. As a consequence, we demonstrate that our approach efficiently and reliably discovers symmetries and orbits of geometric datasets without requiring heavy parameter tuning.
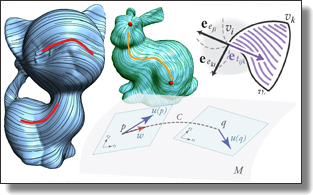	Discrete Connection and Covariant Derivative for Vector Field Analysis and Design Beibei Liu, Yiying Tong, Fernando de Goes, and Mathieu Desbrun. ACM Trans. Graph, 35(3), Art. 23, 2016. Abstract: In this paper, we introduce a discrete definition of connection on simplicial manifolds, involving closed-form continuous expressions within simplices and finite rotations across simplices. The finite-dimensional parameters of this connection are optimally computed by minimizing a quadratic measure of the deviation to the (discontinuous) Levi-Civita connection induced by the embedding of the input triangle mesh, or to any metric connection with arbitrary cone singularities at vertices. From this discrete connection, a covariant derivative is constructed through exact differentiation, leading to explicit expressions for local integrals of first-order derivatives (such as divergence, curl and the Cauchy-Riemann operator), and for L2-based energies (such as the Dirichlet energy). We finally demonstrate the utility, flexibility, and accuracy of our discrete formulations for the design and analysis of vector, n-vector, and n-direction fields.
	A Semi-analytical Approach to Molecular Dynamics Dominik L. Michels and Mathieu Desbrun. J. of Computational Physics, Vol. 303, Pages 336-354, December 2015. Abstract: Despite numerous computational advances over the last few decades, molecular dynamics still favors explicit (and thus easily-parallelizable) time integrators for large scale numerical simulation. As a consequence, computational efficiency in solving its typically stiff oscillatory equations of motion is hampered by stringent stability requirements on the time step size. In this paper, we present a semianalytical integration scheme that others a total speedup of a factor 30 compared to the Verlet method on typical MD simulation by allowing over three orders of magnitude larger step sizes. By efficiently approximating the exact integration of the strong (harmonic) forces of covalent bonds through matrix functions, far improved stability with respect to time step size is achieved without sacrificing the explicit, symplectic, time-reversible, or fine-grained parallelizable nature of the integration scheme. We demonstrate the efficiency and scalability of our integrator on simulations ranging from DNA strand unbinding and protein folding to nanotube resonators.
	Time-Varying Surface Reconstruction of an Actor’s Performance Ludovic Blache, Mathieu Desbrun, Céline Loscos, and Laurent Lucas. Advances in Visual Computing, Volume 9474 of Lecture Notes in Computer Science, 92-101, December 2015. Abstract: We propose a fully automatic time-varying surface reconstruction of an actor’s performance captured from a production stage through omnidirectional video. The resulting mesh and its texture can then directly be edited in post-production. Our method makes no assumption on the costumes or accessories present in the recording. We take as input a raw sequence of volumetric static poses reconstructed from video sequences acquired in a multi-viewpoint chroma-key studio. The first frame is chosen as the reference mesh. An iterative approach is applied throughout the sequence in order to induce a deformation of the reference mesh for all input frames. At first, a pseudo-rigid transformation adjusts the pose to match the input visual hull as closely as possible. Then, local deformation is added to reconstruct fine details. We provide examples of actors’ performance inserted into virtual scenes, including dynamic interaction with the environment.
	Model-Reduced Variational Fluid Simulation Beibei Liu, Gemma Mason, Julian Hodgson, Yiying Tong, and Mathieu Desbrun. ACM Trans. Graph. (SIG Asia), 34(6), Art. 244, November 2015. Abstract: We present a model-reduced variational Eulerian integrator for incompressible fluids, which combines the efficiency gains of dimension reduction, the qualitative robustness of coarse spatial and temporal resolutions of geometric integrators, and the simplicity of sub-grid accurate boundary conditions on regular grids to deal with arbitrarily-shaped domains. At the core of our contributions is a functional map approach to fluid simulation for which scalar- and vector-valued eigenfunctions of the Laplacian operator can be easily used as reduced bases. Using a variational integrator in time to preserve liveliness and a simple, yet accurate embedding of the fluid domain onto a Cartesian grid, our model-reduced fluid simulator can achieve realistic animations in significantly less computational time than full-scale non-dissipative methods but without the numerical viscosity from which current reduced methods suffer. We also demonstrate the versatility of our approach by showing how it easily extends to magnetohydrodynamics and turbulence modeling in 2D, 3D and curved domains.
	Vector field processing on triangle meshes Fernando de Goes, Mathieu Desbrun, and Yiying Tong. Course notes, ACM SIGGRAPH Asia 2015. Abstract: While scalar fields on surfaces have been staples of geometry processing, the use of tangent vector fields has steadily grown in geometry processing over the last two decades: they are crucial to encoding directions and sizing on surfaces as commonly required in tasks such as texture synthesis, non-photorealistic rendering, digital grooming, and meshing. There are, however, a variety of discrete representations of tangent vector fields on triangle meshes, and each approach offers different trade-offs among simplicity, efficiency, and accuracy depending on the targeted application. This course reviews the three main families of discretizations used to design computational tools for vector field processing on triangle meshes: face-based, edge-based, and vertex-based representations. In the process of reviewing the computational tools offered by these representations, we go over a large body of recent developments in vector field processing in the area of discrete differential geometry. We also discuss the theoretical and practical limitations of each type of discretization, and cover increasingly-common extensions such as n-direction and n-vector fields. While the course will focus on explaining the key approaches to practical encoding and manipulation of finite-dimensional vector fields, important differential geometric notions will also be covered: as often in Discrete Differential Geometry, the discrete picture will be used to illustrate deep continuous concepts such as covariant derivatives, metric connections, or Bochner Laplacians.
	Power Particles: An incompressible fluid solver based on power diagrams Fernando de Goes, Corentin Wallez, Jin Huang, Dmitry Pavlov, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH),34(4), Art. 50, 2015. Video part I, part II Abstract: This paper introduces a new particle-based approach to incompressible fluid simulation. We depart from previous Lagrangian methods by considering fluid particles no longer purely as material points, but also as volumetric parcels that partition the fluid domain. The fluid motion is described as a time series of well-shaped power diagrams (hence the name power particles), offering evenly spaced particles and accurate pressure computations. As a result, we circumvent the typical excess damping arising from kernel-based evaluations of internal forces or density without having recourse to auxiliary Eulerian grids. The versatility of our solver is demonstrated by the simulation of multiphase flows and free surfaces.
	Frame Field Generation through Metric Customization Tengfei Jiang, Xianzhong Fang, Jin Huang, Hujun Bao, Yiying Tong, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH), 34(4), Art. 40, 2015. Abstract: This paper presents a new technique for frame field generation. As generic frame fields (with arbitrary anisotropy, orientation, and sizing) can be regarded as cross fields in a specific Riemannian metric, we tackle frame field design by first computing a discrete metric on the input surface that is compatible with a sparse or dense set of input constraints. The final frame field is then found by computing an optimal cross field in this customized metric. We propose frame field design constraints on alignment, size, and skewness at arbitrary locations on the mesh as well as along feature curves, offering much improved flexibility over previous approaches. We demonstrate the advantages of our frame field generation through the automatic quadrangulation of man-made and organic shapes with controllable anisotropy, robust handling of narrow surface strips, and precise feature alignment. We also extend our technique to the design of n-vector fields.
	Computational Electromagnetism with Variational Integrators and Discrete Differential Forms Ari Stern, Yiying Tong, Mathieu Desbrun, and Jerrold E. Marsden. In Geometry, mechanics, and dynamics: the legacy of Jerry Marsden, Fields Institute Communications, 2014. Abstract: In this paper, we introduce a general family of variational, multisymplectic numerical methods for solving Maxwell's equations, using discrete differential forms in spacetime. In doing so, we demonstrate several new results, which apply both to some well-established numerical methods and to new methods introduced here. First, we show that Yee's finite-difference time-domain (FDTD) scheme, along with a number of related methods, are multisymplectic and derive from a discrete Lagrangian variational principle. Second, we generalize the Yee scheme to unstructured meshes, not just in space, but in 4-dimensional spacetime. This relaxes the need to take uniform time steps, or even to have a preferred time coordinate at all. Finally, as an example of the type of methods that can be developed within this general framework, we introduce a new asynchronous variational integrator (AVI) for solving Maxwell's equations. These results are illustrated with some prototype simulations that show excellent energy and conservation behavior.
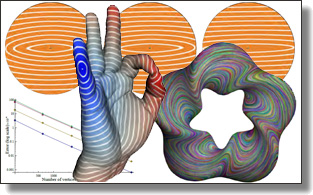	Discrete 2-Tensor Fields on Triangulations Fernando de Goes, Beibei Liu, Max Budninskiy, Yiying Tong, and Mathieu Desbrun. Symposium on Geometry Processing, CGF, 33(5):13-24, 2014. Abstract: Geometry processing has made ample use of discrete representations of tangent vector fields and antisymmetric tensors (i.e., forms) on triangulations. Symmetric 2-tensors, while crucial in the definition of inner products and elliptic operators, have received only limited attention. They are often discretized by first defining a coordinate system per vertex, edge or face, then storing their components in this frame field. In this paper, we introduce a representation of arbitrary 2-tensor fields on triangle meshes. We leverage a coordinate-free decomposition of continuous 2-tensors in the plane to construct a finite-dimensional encoding of tensor fields through scalar values on oriented simplices of a manifold triangulation. We also provide closed-form expressions of pairing, inner product, and trace for this discrete representation of tensor fields, and formulate a discrete covariant derivative and a discrete Lie bracket. Our approach extends discrete/finite-element exterior calculus, recovers familiar operators such as the weighted Laplacian operator, and defines discrete notions of divergence-free, curl-free, and traceless tensors—thus offering a numerical framework for discrete tensor calculus on triangulations. We finally demonstrate the robustness and accuracy of our operators on analytical examples, before applying them to the computation of anisotropic geodesic distances on discrete surfaces.
	Fast Tile-Based Adaptive Sampling with User-Specified Fourier Spectra Florent Wachtel, Adrien Pilleboue, David Coeurjolly, Katherine Breeden, Gurprit Singh, Gael Cathelin, Fernando de Goes, Mathieu Desbrun, and Victor Ostromoukhov. ACM Transactions on Graphics (SIGGRAPH), Vol. 33(4), Art. 56, 2014. (see also Project Page (with code and data), supplementary material, and video) Abstract: We introduce a fast tile-based method for adaptive two-dimensional sampling with user-specified spectral properties. At the core of our approach is a deterministic, hierarchical construction of self-similar, equi-area, tri-hex tiles whose centroids have a spatial distribution free of spurious spectral peaks. A lookup table of sample points, computed offline using any existing point set optimizer to shape the samples’ Fourier spectrum, is then used to populate the tiles. The result is a linear-time, adaptive, and high-quality sampling of arbitrary density functions that conforms to the desired spectral distribution, achieving a speed improvement of several orders of magnitude over current spectrum-controlled sampling methods.
	Space-Time Editing of Elastic Motion through Material Optimization and Reduction Siwang Li, Jin Huang, Fernando de Goes, Xiaogang Jin, Hujun Bao, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH), Vol. 33(4), Art. 108, 2014. (video) Abstract: We present a novel method for elastic animation editing with spacetime constraints. In a sharp departure from previous approaches, we not only optimize control forces added to a linearized dynamic model, but also optimize material properties to better match user constraints and provide plausible and consistent motion. Our approach achieves efficiency and scalability by performing all computations in a reduced rotation-strain (RS) space constructed with both cubature and geometric reduction, leading to two orders of magnitude improvement over the original RS method. We demonstrate the utility and versatility of our method in various applications, including motion editing, pose interpolation, and estimation of material parameters from existing animation sequences.
	A Constructive Theory of Sampling for Image Synthesis using Reproducing Kernel Bases Christian Lessig, Mathieu Desbrun, and Eugene Fiume. ACM Transactions on Graphics (SIGGRAPH), Vol. 33(4), Art. 66, 2014 (see also Project Page). Abstract: Sampling a scene by tracing rays and reconstructing an image from such pointwise samples is fundamental to computer graphics. To improve the efficacy of these computations, we propose an alternative theory of sampling. In contrast to traditional formulations for image synthesis, which appeal to nonconstructive Dirac deltas, our theory employs constructive reproducing kernels for the correspondence between continuous functions and pointwise samples. Conceptually, this allows us to obtain a common mathematical formulation of almost all existing numerical techniques for image synthesis. Practically, it enables novel sampling based numerical techniques designed for light transport that provide considerably improved performance per sample. We exemplify the practical benefits of our formulation with three applications: pointwise transport of color spectra, projection of the light energy density into spherical harmonics, and approximation of the shading equation from a photon map. Experimental results verify the utility of our sampling formulation, with lower numerical error rates and enhanced visual quality compared to existing techniques.
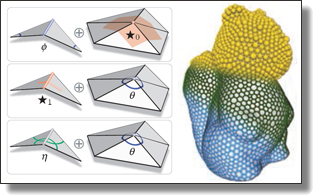	Weighted Triangulations for Geometry Processing Fernando de Goes, Pooran Memari, Patrick Mullen, and Mathieu Desbrun. ACM Transactions on Graphics, Vol. 33 (3). Art. 28, 2014. Abstract: In this paper, we investigate the use of weighted triangulations as discrete, augmented approximations of surfaces for digital geometry processing. By incorporating a scalar weight per mesh vertex, we introduce a new notion of discrete metric that defines an orthogonal dual structure for arbitrary triangle meshes and thus extends weighted Delaunay triangulations to surface meshes. We also present alternative characterizations of this primal-dual structure (through combinations of angles, areas, and lengths) and, in the process, uncover closed-form expressions of mesh energies that were previously known in implicit form only. Finally, we demonstrate how weighted triangulations provide a faster and more robust approach to a series of geometry processing applications, including the generation of well-centered meshes, self-supporting surfaces, and sphere packing.
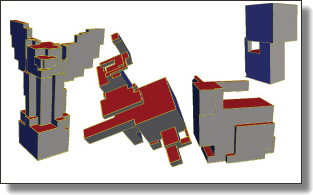	ℓ₁-based Construction of Polycube Maps from Complex Shapes Jin Huang, Tengfei Jiang, Zeyun Shi, Yiying Tong, Hujun Bao, and Mathieu Desbrun. ACM Transactions on Graphics, Vol. 33(3), Art. 25, 2014. Abstract: Polycube maps of triangle meshes have proved useful in a wide range of applications including texture mapping and hexahedral mesh generation. However, constructing either fully automatically or with limited user control a low-distortion polycube from a detailed surface remains challenging in practice. We propose a variational method for deforming an input triangle mesh into a polycube shape through minimization of the ℓ₁-norm of the mesh normals, regularized via an as-rigid-as-possible volumetric distortion energy. Unlike previous work, our approach makes no assumption on the orientation, or on the presence of features in the input model. User-guided control over the resulting polycube map is also offered to increase design flexibility. We demonstrate the robustness, efficiency and controllability of our method on a variety of examples, and explore applications in hexahedral remeshing and quadrangulation.
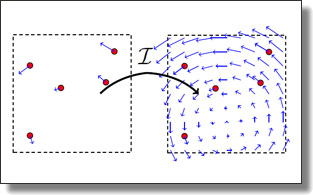	On the Coupling Between an Ideal Fluid and Immersed Particles Henry O. Jacobs, Tudor S. Ratiu, and Mathieu Desbrun. Physica D, 265(15), pp. 40–56, December 2013. Abstract: In this paper we present finite dimensional particle-based models for fluids which respect a number of geometric properties of the Euler equations of motion. Specifically, we use Lagrange-Poincaré reduction to understand the coupling between a fluid and a set of Lagrangian particles that are supposed to simulate it. We substitute the use of principal connections in [Cendra et al. 2001] with vector field valued interpolations from particle velocity data. The consequence of writing evolution equations in terms of interpolation is two-fold. First, it provides estimates on the error incurred when interpolation is used to derive the evolution of the system. Second, this form of the equations of motion can inspire a family of particle and hybrid particle-spectral methods, where the error analysis is "built-in''. We also discuss the influence of other parameters attached to the particles, such as shape, orientation, or higher-order deformations, and how they can help with conservation of momenta in the sense of Kelvin's circulation theorem.
	On the Equilibrium of Simplicial Masonry Structures Fernando de Goes, Pierre Alliez, Houman Owhadi, and Mathieu Desbrun ACM Transactions on Graphics (SIGGRAPH) 32(4), Art. 93, 2013 Abstract: We present a novel approach for the analysis and design of selfsupporting simplicial masonry structures. A finite-dimensional formulation of their compressive stress field is derived, offering a new interpretation of thrust networks through numerical homogenization theory. We further leverage geometric properties of the resulting force diagram to identify a set of reduced coordinates characterizing the equilibrium of simplicial masonry. We finally derive computational form-finding tools that improve over previous work in efficiency, accuracy, and scalability.
	The Chain Collocation Method: A Spectrally Accurate Calculus of Forms Dzhelil Rufat, Gemma Mason, Patrick Mullen, and Mathieu Desbrun. Journal of Computational Physics, Volume 257(B), Pages 1352–1372, 2014.[Project page] Abstract: Preserving in the discrete realm the underlying geometric, topological, and algebraic structures at stake in partial differential equations has proven to be a fruitful guiding principle for numerical methods in a variety of fields such as elasticity, electromagnetism, or fluid mechanics. However, structure-preserving methods have traditionally used spaces of piecewise polynomial basis functions for differential forms. Yet, in many problems where solutions are smoothly varying in space, a spectral numerical treatment is called for. In an effort to provide structure-preserving numerical tools with spectral accuracy on logically rectangular grids over periodic or bounded domains, we present a spectral extension of the discrete exterior calculus (DEC), with resulting computational tools extending well-known collocation-based spectral methods. Its efficient implementation using fast Fourier transforms is provided as well.
	Digital Geometry Processing using Discrete Exterior Calculus Fernando de Goes, Keenan Crane, Peter Schröder, and Mathieu Desbrun ACM SIGGRAPH'13 Course Notes (see also Keenan's page). Abstract: An introduction to geometry processing using discrete exterior calculus (DEC), which provides a simple, flexible, and efficient framework for building a unified geometry-processing platform. The course provides essential mathematical background as well as a large array of real-world examples. It also provides a short survey of the most relevant recent developments in digital geometry processing and discrete differential geometry. Compared to previous SIGGRAPH courses, this course focuses heavily on practical aspects of DEC, with an emphasis on implementation and applications. The course begins with the core ideas from exterior calculus, in both the smooth and discrete setting. Then it shows how a large number of fundamental geometry-processing tools (smoothing, parameterization, geodesics, mesh optimization, etc) can be implemented quickly, robustly, and efficiently within this single common framework. It concludes with a discussion of recent extensions of DEC that improve efficiency, accuracy, and versatility. The course notes grew out of the discrete differential geometry course taught over the past five years at the California Institute of Technology, for undergraduates and beginning graduate students in computer science, applied mathematics, and associated fields. The notes also provide guided exercises (both written and coding) that attendees can later use to deepen their understanding of the material.
	Variational Discretization for Rotating Stratified Fluids Mathieu Desbrun, Evan S. Gawlik, François Gay-Balmaz, and Vladimir Zeitlin AIMS Discrete & Continuous Systems Series A, 34(2), pp. 477-509, Feb 2014 Abstract. In this paper we develop and test a structure-preserving discretization scheme for rotating and/or stratified fluid dynamics. The numerical scheme is based on a finite dimensional approximation of the group of volume preserving diffeomorphisms and is derived via a discrete version of the Euler-Poincaré variational formulation of rotating stratified fluids. The resulting variational integrator allows for a discrete version of Kelvin circulation theorem, is applicable to irregular meshes and, being symplectic, exhibits excellent long term energy behavior. We then report a series of preliminary tests for rotating stratified flows in configurations that are symmetric with respect to translation along one of the spatial directions. In the benchmark processes of hydrostatic and/or geostrophic adjustments, these tests show that the slow and fast component of the flow are correctly reproduced. The harder test of inertial instability is in full agreement with the common knowledge of the process of development and saturation of this instability, while preserving energy nearly perfectly and respecting conservation laws.
	Interactive Elastic Motion Editing through Spacetime Position Constraints Siwang Li, Jin Huang, Mathieu Desbrun. and Xiaogang Jin Journal of Computer Animation and Virtual Worlds (CASA), 2013 Abstract: We present an intuitive and interactive approach for motion editing through spacetime constraints on positions. Given an input motion of an elastic body, our approach enables the user to interactively edit node positions in order to alter and fine-tune the motion. We formulate our motion editing as an optimization problem with dynamics constraints to enforce a physically-plausible result. Through linearization of the editing around the input trajectory, we simplify this constrained optimal control problem into an unconstrained quadratic optimization. The optimal motion thus becomes the solution of a dense linear system, which we solve efficiently by applying the adjoint method in each iteration of a conjugate gradient solver. We demonstrate the efficiency and quality of our motion editing technique on a series of examples.
	Feature-Preserving Surface Reconstruction and Simplification from Defect-Laden Point Sets Julie Digne, David Cohen-Steiner, Pierre Alliez, Mathieu Desbrun, and Fernando de Goes Journal of Mathematical Imaging and Vision, Springer, Jan 2013 Abstract: We introduce a robust and feature-capturing surface reconstruction and simplification method that turns an input point set into a low triangle-count simplicial complex. Our approach starts with a (possibly non-manifold) simplicial complex filtered from a 3D Delaunay triangulation of the input points. This initial approximation is iteratively simplified based on an error metric that measures, through optimal transport, the distance between the input points and the current simplicial complex—both seen as mass distributions. Our approach is shown to exhibit both robustness to noise and outliers, as well as preservation of sharp features and boundaries. Our new feature-sensitive metric between point sets and triangle meshes can also be used as a post-processing tool that, from the smooth output of a reconstruction method, recovers sharp features and boundaries present in the initial point set.
	Blue Noise through Optimal Transport Fernando de Goes, Katherine Breeden, Victor Ostromoukhov, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH Asia), 2012 [Project page] Abstract: We present a fast, scalable algorithm to generate high-quality blue noise point distributions of arbitrary density functions. At its core is a novel formulation of the recently-introduced concept of capacity-constrained Voronoi tessellation as an optimal transport problem. This insight leads to a continuous formulation able to enforce the capacity constraints exactly, unlike previous work. We exploit the variational nature of this formulation to design an efficient optimization technique of point distributions via constrained minimization in the space of power diagrams. Our mathematical, algorithmic, and practical contributions lead to high-quality blue noise point sets with improved spectral and spatial properties.
	Modeling Across Scales: Discrete Geometric Structures in Homogenization and Inverse Homogenization Mathieu Desbrun, Roger Donaldson, and Houman Owhadi. In Multiscale Analysis and Nonlinear Dynamics Reviews of Nonlinear Dynamics and Complexity (Volume 8), Wiley, 2013. See also [arXiv 0904.2601] Abstract: Imaging and simulation methods are typically constrained to resolutions much coarser than the scale of physical micro-structures present in body tissues or geological features. Mathematical and numerical homogenization address this practical issue by identifying and computing appropriate spatial averages that result in accuracy and consistency between the macro-scales we observe and the underlying micro-scale models we assume. Among the various applications benefiting from homogenization, Electric Impedance Tomography (EIT) images the electrical conductivity of a body by measuring electrical potentials consequential to electric currents applied to the exterior of the body. EIT is routinely used in breast cancer detection and cardio-pulmonary imaging, where current flow in fine-scale tissues underlies the resulting coarse-scale images. In this paper, we introduce a geometric approach for the homogenization (simulation) and inverse homogenization (imaging) of divergence-form elliptic operators with rough conductivity coefficients in dimension two. We show that conductivity coefficients are in one-to-one correspondence with divergence-free matrices and convex functions over the domain. Although homogenization is a non-linear and non-injective operator when applied directly to conductivity coefficients, homogenization becomes a linear interpolation operator over triangulations of the domain when re-expressed using convex functions, and is a volume averaging operator when re-expressed with divergence-free matrices. We explicitly give the transformations which map conductivity coefficients into divergence-free matrices and convex functions, as well as their respective inverses. Using weighted Delaunay triangulations for linearly interpolating convex functions, we apply this geometric framework to obtain a robust homogenization algorithm for arbitrary rough coefficients, extending the global optimality of Delaunay triangulations with respect to a discrete Dirichlet energy to weighted Delaunay triangulations. We then consider inverse homogenization, which is known to be both non-linear and severely ill-posed, but that we can decompose into a linear ill-posed problem and a well-posed non-linear problem. Finally, our new geometric approach to homogenization and inverse homogenization is applied to EIT.
	Tightening the Precision of Perspective Rendering Paul Upchurch and Mathieu Desbrun. Journal of Graphics Tools, Volume 16, Issue 1, 2012. Abstract: Precise depth calculation is of crucial importance in graphics rendering. Improving precision raises the quality of all downstream graphical techniques that rely on computed depth (e.g.,, depth buffers, soft and hard shadow maps, screen space ambient occlusion, and 3D stereo projection). In addition, the domain of correctly renderable scenes is expanded by allowing larger far to near plane ratios and smaller depth separation between mesh elements. Depth precision is an ongoing problem as visible artifacts continue to plague applications from interactive games to scientific visualizations despite advances in graphics hardware. In this paper we present and analyze two methods that can greatly impact visual quality by automatically improving the precision of depth values calculated in a standard perspective divide rendering system such as OpenGL® or DirectX®. The methods are easy to implement and compatible with standard depth value calculations.
	Parameterization of Generalized Primal-Dual Triangulations Pooran Memari, Patrick Mullen, and Mathieu Desbrun. International Meshing Roundtable, 2011. Abstract: Motivated by practical numerical issues in a number of modeling and simulation problems, we introduce the notion of a compatible dual complex to a primal triangulation, such that a simplicial mesh and its compatible dual complex (made out of convex cells) form what we call a primal-dual triangulation. Using algebraic and computational geometry results, we show that compatible dual complexes exist only for a particular type of triangulation known as weakly regular. We also demonstrate that the entire space of primal-dual triangulations, which extends the well known (weighted) Delaunay/Voronoi duality, has a convenient, geometric parametrization. We finally discuss how this parametrization may play an important role in discrete optimization problems such as optimal mesh generation, as it allows us to easily explore the space of primal-dual structures along with some important subspaces.
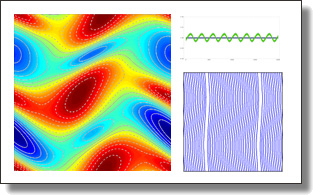	Geometric, Variational Discretization of Continuum Theories Evan Gawlik, Patrick Mullen, Dmitry Pavlov, Jerrold E. Marsden, and Mathieu Desbrun. Physica D: Nonlinear Phenomena, 240(21), 1724-1760, 2011. Abstract: This study derives geometric, variational discretizations of continuum theories arising in fluid dynamics, magnetohydrodynamics (MHD), and the dynamics of complex fluids. A central role in these discretizations is played by the geometric formulation of fluid dynamics, which views solutions to the governing equations for perfect fluid flow as geodesics on the group of volume-preserving diffeomorphisms of the fluid domain. Inspired by this framework, we construct a finite-dimensional approximation to the diffeomorphism group and its Lie algebra, thereby permitting a variational temporal discretization of geodesics on the spatially discretized diffeomorphism group. The extension to MHD and complex fluid flow is then made through an appeal to the theory of Euler-Poincaré systems with advection, which provides a generalization of the variational formulation of ideal fluid flow to fluids with one or more advected parameters. Upon deriving a family of structured integrators for these systems, we test their performance via a numerical implementation of the update schemes on a cartesian grid. Among the hallmarks of these new numerical methods are exact preservation of momenta arising from symmetries, automatic satisfaction of solenoidal constraints on vector fields, good long-term energy behavior, robustness with respect to the spatial and temporal resolution of the discretization, and applicability to irregular meshes.
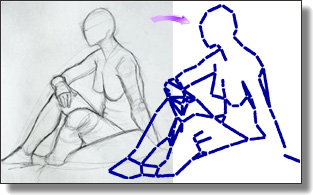	An Optimal Transport Approach to Robust Reconstruction and Simplification of 2D Shapes Fernando de Goes, David Cohen-Steiner, Pierre Alliez, and Mathieu Desbrun. Symposium on Geometry Processing, 2011. Abstract: We propose a robust 2D shape reconstruction and simplification algorithm which takes as input a defect- laden point set with noise and outliers. We introduce an optimal-transport driven approach where the input point set, considered as a sum of Dirac measures, is approximated by a simplicial complex considered as a sum of uniform measures on 0- and 1-simplices. A fine-to-coarse scheme is devised to construct the resulting simplicial complex through greedy decimation of a Delaunay triangulation of the input point set. Our method performs well on a variety of examples ranging from line drawings to grayscale images, with or without noise, features, and boundaries.
	HOT: Hodge-Optimized Triangulations Patrick Mullen, Pooran Memari, Fernando de Goes, Mathieu Desbrun. Transactions on Graphics (SIGGRAPH) 2011. Abstract: We introduce Hodge-optimized triangulations (HOT), a family of well-shaped primal-dual pairs of complexes designed for fast and accurate computations in computer graphics. Previous work most commonly employs barycentric or circumcentric duals; while barycentric duals guarantee that the dual of each simplex lies within the simplex, circumcentric duals are often preferred due to the induced orthogonality between primal and dual complexes. We instead promote the use of weighted duals (power diagrams). They allow greater flexibility in the location of dual vertices while keeping primal-dual orthogonality, thus providing a valuable extension to the usual choices of dual by only adding one additional scalar per primal vertex. Furthermore, we introduce a family of functionals on pairs of complexes that we derive from bounds on the errors induced by diagonal Hodge stars, commonly used in discrete computations. The minimizers of these functionals, called HOT meshes, are shown to be generalizations of Centroidal Voronoi Tesselations and Optimal Delaunay Triangulations, and to provide increased accuracy and flexibility for a variety of computational purposes.
	Exoskeleton: Curve Network Abstraction for 3D Shapes F. de Goes, S. Goldenstein, M. Desbrun, L. Velho. Computer & Graphics, 35(1), February 2011, 112-121. Abstract: In this paper, we introduce the concept of an exoskeleton as a new abstraction of arbitrary shapes that succinctly conveys both the perceptual and the geometric structure of a 3D model. We extract exoskeletons via a principled framework that combines segmentation and shape approximation. Our method starts from a segmentation of the shape into perceptually relevant parts and then constructs the exoskeleton using a novel extension of the Variational Shape Approximation method. Benefits of the exoskeleton abstraction to graphics applications such as simplification and chartification are presented.
	Discrete Lie Advection of Differential Forms P. Mullen, A. McKenzie, D. Pavlov, L. Durant, Y. Tong, E. Kanso, J. E. Marsden, and M. Desbrun. FoCM (Foundations of Computational Mathematics), in press, 2010. Abstract: In this paper, we present a numerical technique for performing Lie advection of arbitrary differential forms. Leveraging advances in high-resolution finite volume methods for scalar hyperbolic conservation laws, we first discretize the interior product (also called~\emph{contraction}) through integrals over Eulerian approximations of extrusions. This, along with Cartan's homotopy formula and a discrete exterior derivative, can then be used to derive a discrete Lie derivative. The usefulness of this operator is demonstrated through the numerical advection of scalar fields and 1-forms on regular grids.
	Interactive Shape Interpolation through Controllable Dynamic Deformation J. Huang, Y. Tong, K. Zhou, H. Bao and M. Desbrun. To appear in Transactions on Visualization and Computer Graphics, 2010. Abstract: In this paper, we introduce an interactive approach to generate physically-based shape interpolation between poses. We extend linear modal analysis to offer an efficient and robust numerical technique to generate physically-plausible dynamics even for very large deformation. Our method also provides a rich set of intuitive editing tools with real-time feedback, including control over vibration frequencies, amplitudes, and damping of the resulting interpolation sequence. We demonstrate the versatility of our approach through a series of complex dynamic shape interpolations.
	Trivial Connections on Discrete Surfaces K. Crane, M. Desbrun, and P.Schröder. Symposium on Geometry Processing (Computer Graphics Forum), 2010. (see also Keenan's project page for code and pictures; SGP Best Paper award) Abstract: This paper presents a straightforward algorithm for constructing connections on discrete surfaces that are as smooth as possible everywhere but on a set of isolated singularities with given index. We compute these connections by solving a single linear system built from standard operators. The solution can be used to design rotationally symmetric direction fields with user-specified singularities and directional constraints.
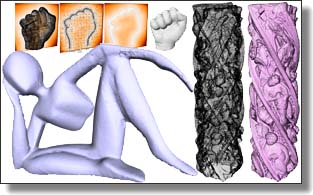	Signing the Unsigned: Robust Surface Reconstruction from Raw Pointsets P. Mullen, F. de Goes, M. Desbrun, D. Cohen-Steiner, and P. Alliez. Symposium on Geometry Processing (to appear in Computer Graphics Forum), 2010. Abstract: We propose a modular framework for robust 3D reconstruction from unorganized, unoriented, noisy, and outlierridden geometric data. We gain robustness and scalability over previous methods through an unsigned distance approximation to the input data followed by a global stochastic signing of the function. An isosurface reconstruction is finally deduced via a sparse linear solve. We show with experiments on large, raw, geometric datasets that this approach is scalable while robust to noise, outliers, and holes. The modularity of our approach facilitates customization of the pipeline components to exploit specific idiosyncracies of datasets, while the simplicity of each component leads to a straightforward implementation.
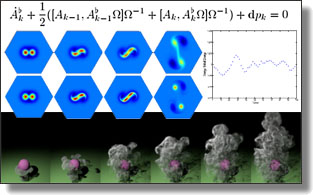	Structure-Preserving Discretization of Incompressible Fluids D. Pavlov, P. Mullen, Y. Tong, E. Kanso, J. E. Marsden, and M. Desbrun. Physica D: Nonlinear Phenomena Volume 240, Issue 6, 1 March 2011, Pages 443-458. Abstract: The geometric nature of Euler fluids has been clearly identified and extensively studied over the years, culminating with Lagrangian and Hamiltonian descriptions of fluid dynamics where the configuration space is defined as the volume-preserving diffeomorphisms, and Kelvin's circulation theorem is viewed as a consequence of Noether's theorem associated with the particle relabeling symmetry of fluid mechanics. However computational approaches to fluid mechanics have been largely derived from a numerical-analytic point of view, and are rarely designed with structure preservation in mind, and often suffer from spurious numerical artifacts such as energy and circulation drift. In contrast, this paper geometrically derives discrete equations of motion for fluid dynamics from first principles in a purely Eulerian form. Our approach approximates the group of volume-preserving diffeomorphisms using a finite dimensional Lie group, and associated discrete Euler equations are derived from a variational principle with non-holonomic constraints. The resulting discrete equations of motion yield a structure-preserving time integrator with good long-term energy behavior and for which an exact discrete Kelvin's circulation theorem holds.
	Deformation Transfer to Multi-Component Objects Kun Zhou, Weiwei Xu, Yiying Tong, and Mathieu Desbrun. Proceedings of Eurographics 2010. (movie) Abstract: We present a simple and effective algorithm to transfer deformation between surface meshes with multiple components. The algorithm automatically computes spatial relationships between components of the target object, builds correspondences between source and target, and finally transfers deformation of the source onto the target while preserving cohesion between the target’s components. We demonstrate the versatility of our approach on various complex models.
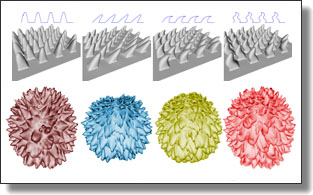	Height and Tilt Geometric Texture Vedrana Andersen, Mathieu Desbrun, J. Andreas Bærentzen, and Henrik Aanæs. Internation Symposium on Visual Computing 2009. Lecture Notes in Computer Science, SpringerVerlag. Abstract: We propose a new intrinsic representation of geometric texture over triangle meshes. Our approach extends the conventional height field texture representation by incorporating displacements in the tangential plane in the form of a normal tilt. This texture representation offers a good practical compromise between functionality and simplicity: it can efficiently handle and process geometric texture too complex to be represented as a height field, without having recourse to full blown mesh editing algorithms. The height-and-tilt representation proposed here is fully intrinsic to the mesh, making texture editing and animation (such as bending or waving) intuitively controllable over arbitrary base mesh. We also provide simple methods for texture extraction and transfer using our height-and-field representation.
	Energy-preserving Integrators for Fluid Animation (corrected version; the pseudocode was missing a term) Patrick Mullen, Keenan Crane, Dmitry Pavlov, Yiying Tong, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH), 28(3), 2009. Abstract: Numerical viscosity has long been a problem in fluid animation. Existing methods suffer from intrinsic artificial dissipation and often apply complicated computational mechanisms to combat such effects. Consequently, dissipative behavior cannot be controlled or modeled explicitly in a manner independent of time step size, complicating the use of coarse previews and adaptive-time stepping methods. This paper proposes simple, unconditionally stable, fully Eulerian integration schemes with no numerical viscosity that are capable of maintaining the liveliness of fluid motion without recourse to corrective devices. Pressure and fluxes are solved efficiently and simultaneously in a time-reversible manner on simplicial grids, and the energy is preserved exactly over long time scales in the case of inviscid fluids. These integrators can be viewed as an extension of the classical energy-preserving Harlow-Welch / Crank- Nicolson scheme to simplicial grids.
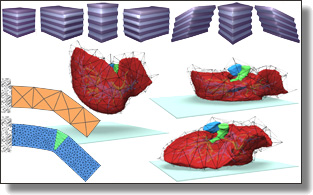	Numerical Coarsening of Inhomogeneous Elastic Materials Lily Kharevych, Patrick Mullen, Houman Owhadi, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH), 28(3), 2009. Abstract: We propose an approach for efficiently simulating elastic objects made of non-homogeneous, non-isotropic materials. Based on recent developments in homogenization theory, a methodology is introduced to approximate a deformable object made of arbitrary fine structures of various linear elastic materials with a dynamically-similar coarse model. This numerical coarsening of the material properties allows for simulation of fine, heterogeneous structures on very coarse grids while capturing the proper dynamics of the original dynamical system, thus saving orders of magnitude in computational time. Examples including inhomogeneous and/or anisotropic materials can be realistically simulated in realtime with a numerically-coarsened model made of a few mesh elements.
	Interleaving Delaunay Refinement and Optimization for Practical Isotropic Tetrahedron Mesh Generation Jane Tournois, Camille Wormser, Pierre Alliez, and Mathieu Desbrun. ACM Transactions on Graphics (SIGGRAPH), 28(3), 2009. Abstract: We present a practical approach to isotropic tetrahedral meshing of 3D domains bounded by piecewise smooth surfaces. Building upon recent theoretical and practical advances, our algorithm interleaves Delaunay refinement and mesh optimization to generate quality meshes that satisfy a set of user-defined criteria. This interleaving is shown to be more conservative in number of Steiner point insertions than refinement alone, and to produce higher quality meshes than optimization alone. A careful treatment of boundaries and their features is presented, offering a versatile framework for designing smoothly graded tetrahedral meshes.
	Lie Group Integrators for Animation and Control of Vehicles Marin Kobilarov, Keenan Crane, and Mathieu Desbrun. To appear in ACM Transactions on Graphics, 2009. (see also Keenan's project page for movies). Abstract: This paper is concerned with the animation and control of vehicles with complex dynamics such as helicopters, boats, and cars. Motivated by recent developments in discrete geometric mechanics we develop a general framework for integrating the dynamics of holonomic and nonholonomic vehicles by preserving their state-space geometry and motion invariants. We demonstrate that the resulting integration schemes are superior to standard methods in numerical robustness and efficiency, and can be applied to many types of vehicles. In addition, we show how to use this framework in an optimal control setting to automatically compute accurate and realistic motions for arbitrary user-specified constraints.
	Variational Integrators for Maxwell's Equations with Sources Ari Stern, Yiying Tong, Mathieu Desbrun, and Jerrold E. Marsden. In Progress in Electromagnetics Research Symposium (PIERS), Vol. 4, No. 7, 711-715, 2008. Abstract: In recent years, two important techniques for geometric numerical discretization have been developed. In computational electromagnetics, spatial discretization has been improved by the use of mixed finite elements and discrete differential forms. Simultaneously, the dynamical systems and mechanics communities have developed structure-preserving time integrators, notably variational integrators that are constructed from a Lagrangian action principle. Here, we discuss how to combine these two frameworks to develop variational spacetime integrators for Maxwell's equations. Extending our previous work, we also show here how to incorporate free sources of charge and current.
	Spectral Conformal Parameterization Patrick Mullen, Yiying Tong, Pierre Alliez, Mathieu Desbrun. Symposium of Geometry Processing, 2008. Abstract: We present a spectral approach to automatically and efficiently obtain discrete free-boundary conformal parameterizations of triangle mesh patches, without the common artifacts due to positional constraints on vertices and without undue bias introduced by sampling irregularity. High-quality parameterizations are computed through a constrained minimization of a discrete weighted conformal energy by finding the largest eigenvalue/eigenvector of a generalized eigenvalue problem involving sparse, symmetric matrices. We demonstrate that this novel and robust approach improves on previous linear techniques both quantitatively and qualitatively.
	Voronoi-based Variational Reconstruction of Unoriented Point Sets Pierre Alliez, David Cohen-Steiner, Yiying Tong, and Mathieu Desbrun. Symposium on Geometry Processing, pp. 39-48, 2007. Abstract: We introduce an algorithm for reconstructing watertight surfaces from unoriented point sets. Using the Voronoi diagram of the input point set, we deduce a tensor field whose principal axes and eccentricities locally represent respectively the most likely direction of the normal to the surface, and the confidence in this direction estimation. An implicit function is then computed by solving a generalized eigenvalue problem such that its gradient is most aligned with the principal axes of the tensor field, providing a best-fitting isosurface reconstruction. Our approach possesses a number of distinguishing features. In particular, the implicit function optimization provides resilience to noise, adjustable fitting to the data, and controllable smoothness of the reconstructed surface. Finally, the use of simplicial meshes (possibly restricted to a thin crust around the input data) and (an)isotropic Laplace operators renders the numerical treatment simple and robust.
	Generalized Surface Flows for Deformable Registration and Cortical Matching Ilya Eckstein, Anand A. Joshi, C.C. Jay Kuo, Richard Leahy, and Mathieu Desbrun. Proceedings of MICCAI, 2007. Abstract: Despite being routinely required in medical applications, deformable surface registration is notoriously difficult due to large intersubject variability and complex geometry of most medical datasets. We present a general and flexible deformable matching framework based on generalized surface flows that efficiently tackles these issues through tailored deformation priors and multiresolution computations. The value of our approach over existing methods is demonstrated for automatic and user-guided cortical registration.
	Generalized Surface Flows for Mesh Processing Ilya Eckstein, Jean-Philippe Pons, Yiying Tong, C.C. Jay Kuo, and Mathieu Desbrun. Symposium on Geometry Processing, pp. 183-192 2007. Abstract: Geometric flows are ubiquitous in mesh processing. Curve and surface evolutions based on functional minimization have been used in the context of surface diffusion, denoising, shape optimization, minimal surfaces, and geodesic paths to mention a few. Such gradient flows are nearly always, yet often implicitly, based on the canonical L2 inner product of vector fields. In this paper, we point out that changing this inner product provides a simple, powerful, and untapped approach to extend current flows. We demonstrate the value of such a norm alteration for regularization and volume-preservation purposes and in the context of shape matching, where deformation priors (ranging from rigid motion to articulated motion) can be incorporated into a gradient flow to drastically improve results. Implementation details, including a differentiable approximation of the Hausdorff distance between irregular meshes, are presented.
	A Discrete Geometric Optimal Control Framework for Systems with Symmetries Marin Kobilarov, Mathieu Desbrun, Jerrold E. Marsden, and Gaurav S. Sukhatme. Proceedings of Robotics: Science and Systems, 2007. Abstract: This paper studies the optimal motion control of mechanical systems through a discrete geometric approach. At the core of our formulation is a discrete Lagrange-d’Alembert-Pontryagin variational principle, from which are derived discrete equations of motion that serve as constraints in our optimization framework. We apply this discrete mechanical approach to holonomic systems with symmetries and, as a result, geometric structure and motion invariants are preserved. We illustrate our method by computing optimal trajectories for a simple model of an air vehicle flying through a digital terrain elevation.
	Design of Tangent Vector Fields (version with no movies here) Matthew Fisher, Peter Schröder, Mathieu Desbrun, and Hugues Hoppe. ACM Trans. on Graphics (SIGGRAPH) 26(3), art. 56, 2007. Abstract: Tangent vector fields are an essential ingredient in controlling surface appearance for applications ranging from anisotropic shading to texture synthesis and non-photorealistic rendering. To achieve a desired effect one is typically interested in smoothly varying fields that satisfy a sparse set of user-provided constraints. Using tools from Discrete Exterior Calculus, we present a simple and efficient algorithm for designing such fields over arbitrary triangle meshes. By representing the field as scalars over mesh edges (i.e., discrete 1-forms), we obtain an intrinsic, coordinate-free formulation in which field smoothness is enforced through discrete Laplace operators. Unlike previous methods, such a formulation leads to a linear system whose sparsity permits efficient pre-factorization. Constraints are incorporated through weighted least squares and can be updated rapidly enough to enable interactive design, as we demonstrate in the context of anisotropic texture synthesis.
	Mesh Puppetry: Cascading Optimization of Mesh Deformation with Inverse Kinematics Xiaohan Shi, Kun Zhou, Yiying Tong, Mathieu Desbrun, Hujun Bao, and Baining Guo. ACM Trans. on Graphics (SIGGRAPH) 26(3), art. 81, 2007. (movie) Abstract: We present mesh puppetry, a variational framework for detail-preserving mesh manipulation through a set of high-level, intuitive, and interactive design tools. Our approach builds upon traditional rigging by optimizing skeleton position and vertex weights in an integrated manner. New poses and animations are created by specifying a few desired constraints on vertex positions, balance of the character, length and rigidity preservation, joint limits, and/or self-collision avoidance. Our algorithm then adjusts the skeleton and solves for the deformed mesh simultaneously through a novel cascading optimization procedure, allowing realtime manipulation of meshes with 50K+ vertices for fast design of pleasing and realistic poses. We demonstrate the potential of our framework through an interactive deformation platform and various applications such as deformation transfer and motion retargeting.
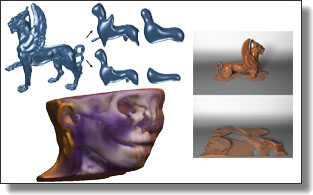	A Variational Approach to Eulerian Geometry Processing Patrick Mullen, Alexander McKenzie, Yiying Tong, and Mathieu Desbrun ACM Trans. on Graphics (SIGGRAPH) 26(3), art. 66, 2007. (movie) Abstract: We present a purely Eulerian framework for geometry processing of surfaces and foliations. Contrary to current Eulerian methods used in graphics, we use conservative methods and a variational interpretation, offering a unified framework for routine surface operations such as smoothing, offsetting, and animation. Computations are performed on a fixed volumetric grid without recourse to Lagrangian techniques such as triangle meshes, particles, or path tracing. At the core of our approach is the use of the Coarea Formula to express area integrals over isosurfaces as volume integrals. This enables the simultaneous processing of multiple isosurfaces, while a single interface can be treated as the special case of a dense foliation. We show that our method is a powerful alternative to conventional geometric representations in delicate cases such as the handling of high-genus surfaces, weighted offsetting, foliation smoothing of medical datasets, and incompressible fluid animation.
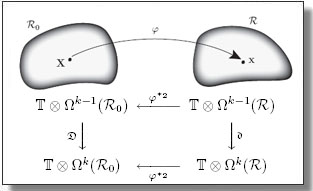	On the Geometric Character of Stress in Continuum Mechanics Eva Kanso, Marino Arroyo, Yiying Tong, Arash Yavari, Jerrold E. Marsden, and Mathieu Desbrun Z. angew. Math. Phys. 58 (2007) 1–14. Abstract: This paper shows that the stress field in the classical theory of continuum mechanics may be taken to be a covector-valued differential two-form. The balance laws and other fundamental laws of continuum mechanics may be neatly rewritten in terms of this geometric stress. A geometrically attractive and covariant derivation of the balance laws from the principle of energy balance in terms of this stress is presented.
	Unconstrained Spherical Parameterization Ilja Friedel, Peter Schröder, and Mathieu Desbrun Journal of Graphics Tools, 12(1), pp. 17-26, 2007. (see also: ACM SIGGRAPH Technical Sketch '05). Abstract: We introduce a novel approach for the construction of spherical parameterizations based on energy minimization. The energies are derived in a general manner from classic formulations well known in the planar parameterization setting (e.g., conformal, Tutte, area, stretch energies, etc), based on the following principles: the energy should (1) be a measure of spherical triangles; (2) treat energies independently of the triangle location on the sphere; and (3) converge to the continuous energy \emph{from above} under refinement. Based on these considerations we give a very simple non-linear modification of standard formulas that fulfills all these requirements. The method avoids the usual collapse of flat energies when they are transferred to the spherical setting without additional constraints (e.g., fixing three or more vertices). Our unconstrained energy minimization problem is amenable to the use of standard solvers. Consequently the implementation effort is minimal while still achieving excellent robustness and performance through the use of widely available numerical minimization software.
	Geometric, Variational Integrators for Computer Animation L. Kharevych, Weiwei, Y. Tong, E. Kanso, J. E. Marsden, P. Schröder, and Mathieu Desbrun ACM/EG Symposium on Computer Animation 2006, pp. 43-51 Abstract: We present a general-purpose numerical scheme for time integration of Lagrangian dynamical systems—an important computational tool at the core of most physics-based animation techniques. Several features make this particular time integrator highly desirable for computer animation: it numerically preserves important invariants, such as linear and angular momenta; the symplectic nature of the integrator also guarantees a correct energy behavior, even when dissipation and external forces are added; holonomic constraints can also be enforced quite simply; finally, our simple methodology allows for the design of high-order accurate schemes if needed. Two key properties set the method apart from earlier approaches. First, the nonlinear equations that must be solved during an update step are replaced by a minimization of a novel functional, speeding up time stepping by more than a factor of two in practice. Second, the formulation introduces additional variables that provide key flexibility in the implementation of the method. These properties are achieved using a discrete form of a general variational principle called the Pontryagin-Hamilton principle, expressing time integration in a discrete geometric manner analog in spirit to geometric modeling techniques to design smooth curves or surfaces. We demonstrate the applicability of our integrators to the simulation of non-linear elasticity with implementation details.
	Designing Quadrangulations with Discrete Harmonic Forms Yiying Tong, Pierre Alliez, David Cohen-Steiner, and Mathieu Desbrun ACM/EG Symposium on Geometry Processing 2006, pp. 201-210 Abstract: We introduce a framework for quadrangle meshing of discrete manifolds. Based on discrete differential forms, our method hinges on extending the discrete Laplacian operator (used extensively in modeling and animation) to allow for line singularities and singularities with fractional indices. When assembled into a singularity graph, these line singularities are shown to considerably increase the design flexibility of quad meshing. In particular, control over edge alignments and mesh sizing are unique features of our novel approach. Another appeal of our method is its robustness and scalability from a numerical viewpoint: we simply solve a sparse linear system to generate a pair of piecewise-smooth scalar fields whose isocontours form a pure quadrangle tiling, with no T-junctions.
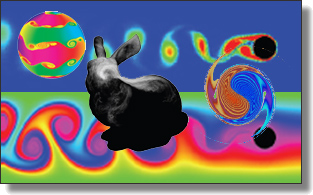	Stable, Circulation-Preserving, Simplicial Fluids Sharif Elcott, Yiying Tong, Eva Kanso, Peter Schröder, and Mathieu Desbrun ACM Transactions on Graphics, 26(1), art. 4, Jan. 2007.(movie) Abstract: Visual quality, low computational cost, and numerical stability are foremost goals in computer animation. An important ingredient in achieving these goals is the conservation of fundamental motion invariants. For example, rigid and deformable body simulation benefits greatly from conservation of linear and angular momenta. In the case of fluids, however, none of the current techniques focuses on conserving invariants, and consequently, they often introduce a visually disturbing numerical diffusion of vorticity. Visually just as important is the resolution of complex simulation domains. Doing so with regular (even if adaptive) grid techniques can be computationally delicate. In this paper, we propose a novel technique for the simulation of fluid flows. It is designed to respect the defining differential properties, i.e., the conservation of circulation along arbitrary loops as they are transported by the flow. Consequently, our method offers several new and desirable properties: arbitrary simplicial meshes (triangles in 2D, tetrahedra in 3D) can be used to define the fluid domain; the computations involved in the update procedure are efficient due to discrete operators with small support; and it preserves discrete circulation avoiding numerical diffusion of vorticity.
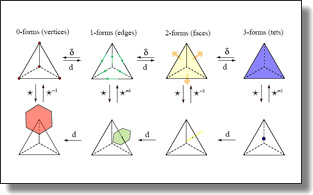	Discrete Differential Forms for Computational Modeling Mathieu Desbrun, Eva Kanso, and Yiying Tong Chapter in ACM SIGGRAPH'05 and '06 Course Notes on Discrete Differential Geometry (revised) Abstract: The emergence of computers as an essential tool in scientific research has shaken the very foundations of differential modeling. Indeed, the deeply-rooted abstraction of smoothness, or differentiability, seems to inherently clash with a computer’s ability of storing only finite sets of numbers. While there has been a series of computational techniques that proposed discretizations of differential equations, the geometric structures they are supposed to simulate are often lost in the process.
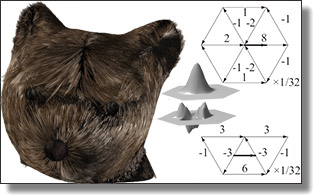	Edge Subdivision Schemes and the Construction of Smooth Vector Fields Ke Wang, Weiwei, Yiying Tong, Mathieu Desbrun, and Peter Schröder ACM Trans. on Graphics (SIGGRAPH '06), 25(3), pp. 1041-1048 Abstract: Vertex- and face-based subdivision schemes are now routinely used in geometric modeling and computational science, and their primal/dual relationships are well studied. In this paper, we interpret these schemes as defining bases for discrete differential 0- resp. 2-forms, and complete the picture by introducing edge-based subdivision schemes to construct the missing bases for discrete differential 1-forms. Such subdivision schemes map scalar coefficients on edges from the coarse to the refined mesh and are intrinsic to the surface. Our construction is based on treating vertex-, edge-, and face-based subdivision schemes as a joint triple and enforcing that subdivision commutes with the topological exterior derivative. We demonstrate our construction for the case of arbitrary topology triangle meshes. Using Loop’s scheme for 0-forms and generalized half-box splines for 2- forms results in a unique generalized spline scheme for 1-forms, easily incorporated into standard subdivision surface codes. We also provide corresponding boundary stencils. Once a metric is supplied, the scalar 1-form coefficients define a smooth tangent vector field on the underlying subdivision surface. Design of tangent vector fields is made particularly easy with this machinery as we demonstrate.
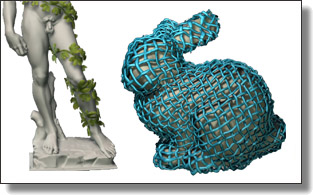	Mesh Quilting For Geometric Texture Synthesis K. Zhou, X. Huang, X. Wang, Y. Tong, M. Desbrun, B. Guo, H.-Y. Sheum In ACM Trans. on Graphics (SIGGRAPH '06). 25(3), pp. 690-697 Abstract: We introduce mesh quilting, a geometric texture synthesis algorithm in which a 3D texture sample given in the form of a triangle mesh is seamlessly applied inside a thin shell around an arbitrary surface through local stitching and deformation. We show that such geometric textures allow interactive and versatile editing and animation, producing compelling visual effects that are difficult to achieve with traditional texturing methods. Unlike pixel-based image quilting, mesh quilting is based on stitching together 3D geometry elements. Our quilting algorithm finds corresponding geometry elements in adjacent texture patches, aligns elements through local deformation, and merges elements to seamlessly connect texture patches. For mesh quilting on curved surfaces, a critical issue is to reduce distortion of geometry elements inside the 3D space of the thin shell. To address this problem we introduce a low-distortion parameterization of the shell space so that geometry elements can be synthesized even on very curved objects without the visual distortion present in previous approaches. We demonstrate how mesh quilting can be used to generate convincing decorations for a wide range of geometric textures.
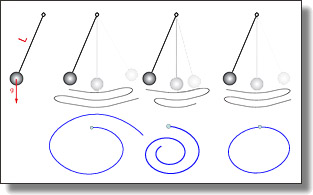	Discrete Geometric Mechanics for Variational Integrators (A Primer for CS) Ari Stern, and Mathieu Desbrun Chapter in ACM SIGGRAPH'06 Course Notes on Discrete Differential Geometry Abstract: In this chapter, we present a geometric---instead of a traditional numerical-analytic---approach to the problem of time integration. Geometry at its most abstract is the study of symmetries and their associated invariants. Variational approaches based on such notions are commonly used in geometric modeling and discrete differential geometry. Here we will treat mechanics in a similar way. Indeed, the very essence of a mechanical system is characterized by its symmetries and invariants. Thus preserving these symmetries and invariants (e.g., certain momenta) into the discrete computational setting is of paramount importance if one wants discrete time integration to properly capture the underlying continuous motion. Motivated by the well-known variational and geometric nature of most dynamical systems, we review the use of discrete variational principles as a way to derive robust, and accurate time integrators.
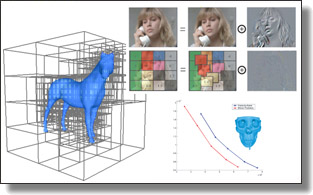	Compression of Time Varying Isosurfaces Ilya Eckstein, Mathieu Desbrun, and C.C. Jay Kuo In Graphics Interface '06, pp. 99-105 Abstract: Compressing sequences of complex time-varying surfaces as generated by medical instrumentations or complex physical simulations can be extremely challenging: repeated topology changes during the surface evolution render most of the previous techniques for compression of time-varying surfaces inefficient or impractical. In order to provide a viable solution, we propose a new approach based upon an existing isosurface compression technique designed for static surfaces. We exploit temporal coherence of the data by adopting the paradigm of block-based motion prediction developed in video coding and extending it using local surface registration. The resulting prediction errors across frames are treated as a static isosurface and encoded progressively using an adaptive octree-based scheme. We also exploit local spatiotemporal patterns through context-based arithmetic coding. Fine-grain geometric residuals are encoded separately with user-specified precision. The other design choices made to handle large datasets are detailed.
	Discrete Differential Geometry: An Applied Introduction Eitan Grinspun, Peter Schröder, and Mathieu Desbrun ACM SIGGRAPH'05 Course Notes (see also: DDG Forum). Slides: Calculus on Meshes, Discrete Differential Fluids, and Meshing Abstract: This volume documents the full day course Discrete Differential Geometry: An Applied Introduction presented at SIGGRAPH ’05 on July 31st, 2005. These notes supplement the lectures given by Mathieu Desbrun, Eitan Grinspun, and Peter Schr¨oder, compiling contributions from: Pierre Alliez, Alexander Bobenko, David Cohen-Steiner, Sharif Elcott, Eva Kanso, Liliya Kharevych, Adrian Secord, John M. Sullivan, Yiying Tong, Mariette Yvinec.
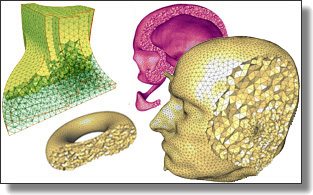	Variational Tetrahedral Meshing Pierre Alliez, David Cohen-Steiner, Mariette Yvinec, and Mathieu Desbrun ACM Trans. on Graphics (SIGGRAPH '05), 24(3), pp. 617-625 Abstract: In this paper, a novel Delaunay-based variational approach to isotropic tetrahedral meshing is presented. To achieve both robustness and efficiency, we minimize a simple mesh-dependent energy through global updates of both vertex positions and connectivity. As this energy is known to be the L1 distance between an isotropic quadratic function and its linear interpolation on the mesh, our minimization procedure generates well-shaped tetrahedra. Mesh design is controlled through a gradation smoothness parameter and selection of the desired number of vertices. We provide the foundations of our approach by explaining both the underlying variational principle and its geometric interpretation. We demonstrate the quality of the resulting meshes through a series of examples.
	TextureMontage: Seamless Texturing of Surfaces From Multiple Images Kun Zhou, Xi Wang, Yiying Tong, Mathieu Desbrun, Baining Guo, and H.-Y. Shum ACM Trans. on Graphics (SIGGRAPH '05), 24(3), pp. 1148-1155. Abstract: We propose a technique, called TextureMontage, to seamlessly map a patchwork of texture images onto an arbitrary 3D model. A texture atlas can be created through the specification of a set of correspondences between the model and any number of texture images. First, our technique automatically partitions the mesh and the images, driven solely by the choice of feature correspondences. Most charts will then be parameterized over their corresponding image planes through the minimization of a distortion metric based on both geometric distortion and texture mismatch across patch boundaries and images. Lastly, a surface texture inpainting technique is used to fill in the remaining charts of the surface with no corresponding texture patches. The resulting texture mapping satisfies the (sparse or dense) user-specified constraints while minimizing the distortion of the texture images and ensuring a smooth transition across the boundaries of different mesh patches.
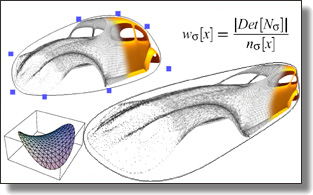	Barycentric Coordinates for Convex Sets Joe Warren, Scott Schaefer, Anil Hirani, and Mathieu Desbrun Advances in Computational Mathematics 27(3) (2007), 319--338. Abstract: Convex Sets Barycentric coordinates are one of the most basic mathematical tools in graphics, as well as in many computational sciences. Although the formulas for simplices (triangles, tetrahedra and so on) are widely known and routinely used, there has been no satisfactory extension of these to arbitrary convex polytopes despite a plethora of potential applications. In this paper, we propose a simple, computationally convenient formula of a canonical form of barycentric coordinates. These functions are rational, smooth and of low degree. Next, we extend the formulas for convex polytopes to smooth, convex functions. Finally, we present an application of barycentric coordinates to free-form deformation.
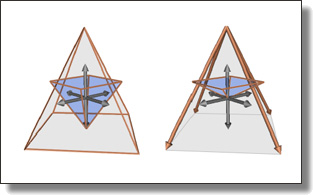	A Geometric Construction of Coordinates for Convex Polyhedra using Polar Duals Tao Ju, Scott Schaefer, Joe Warren, and Mathieu Desbrun ACM SIGGRAPH/EG Symposium of Geometry Processing 2005, pp. 181-186. Abstract: A fundamental problem in geometry processing is that of expressing a point inside a convex polyhedron as a combination of the vertices of the polyhedron. Instances of this problem arise often in mesh parameterization and 3D deformation. A related problem is to express a vector lying in a convex cone as a non-negative combination of edge rays of this cone. This problem also arises in many applications such as planar graph embedding and spherical parameterization. In this paper, we present a unified geometric construction for building these weighted combinations using the notion of polar duals. We show that our method yields a simple geometric construction for Wachspress’s barycentric coordinates, as well as for constructing Colin de Verdière matrices from convex polyhedra—a critical step in Lovasz’s method with applications to parameterizations.
	Vector Field Analysis and Visualization through Variational Clustering Alexander McKenzie, Santiago Lombeyda, Mathieu Desbrun EG - IEEE VGTC Symposium on Visualization (2005), 1-–7. Abstract: Scientific computing is an increasingly crucial component of research in various disciplines. Despite its potential, exploration of the results is an often laborious task, owing to excessively large and verbose datasets output by these simulation runs. Several approaches have been proposed to analyze, classify, and simplify such data to facilitate an informative visualization and deeper understanding of the underlying system. However, traditional methods leave much room for improvement. In this article we investigate the visualization of large vector fields, departing from accustomed processing algorithms by casting vector field simplification as a variational partitioning problem. Adopting an iterative strategy, we introduce the notion of vector “proxies” to minimize the distortion error of our simplification by clustering the dataset into multiple best-fitting characteristic regions. This error driven approach can be performed with respect to various similarity metrics, offering a convenient set of tools to design clear and succinct representations of high dimensional datasets. We illustrate the benefits of such tools through visualization experiments of three-dimensional vector fields.
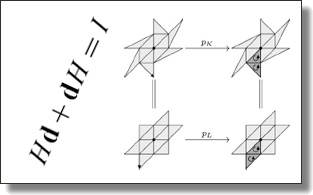	Discrete Poincaré Lemma Mathieu Desbrun, Melvin Leok, Jerrold E. Marsden Applied Numerical Mathematics 53 (2005) 231–248. Abstract: This paper proves a discrete analogue of the Poincaré lemma in the context of a discrete exterior calculus based on simplicial cochains. The proof requires the construction of a generalized cone operator as the geometric cone of a simplex cannot, in general, be interpreted as a chain in the simplicial complex. The corresponding cocone operatorcan be shown to be a homotopy operator, and this yields the discrete Poincaré lemma. The generalized cone operator is a combinatorial operator that can be constructed for any simplicial complex that can be grown by a process of local augmentation. In particular, regular triangulations and tetrahedralizations in R^2 and R^3 are presented, for which the discrete Poincaré lemma is globally valid.
	Geodesics-based One-to-One Parameterization of 3D Triangle Meshes Haeyoung Lee, Yiying Tong, and Mathieu Desbrun IEEE Multimedia journal, Volume 12, Issue 1, Jan.-March 2005, 27--33. Abstract: Digital geometry is a new data type for multimedia applications. To foster the use of 3D geometry, we introduce a piecewise linear parameterization of 3D surfaces that we can use for texture mapping, morphing, remeshing, and geometry imaging. Our method guarantees one-to-one mapping without foldovers in a geometrically intuitive way.
	A Haptic-Rendering Technique Based on Hybrid Surface Representation Laehyun Kim, Gaurav Sukhatme, and Mathieu Desbrun IEEE Computer Graphics and Applications Volume 24, Number 2, March/April 2004, 66--75. Abstract: Our novel haptic rendering technique using a hybrid surface representation addresses conventional limitations in haptic displays.
	Removing Excess Topology From Isosurfaces Zoë Wood, Hugues Hoppe, Mathieu Desbrun and Peter Schröder ACM Trans. on Graphics, 23(2), pp. 190 - 203, April 2004 Abstract: Many high-resolution surfaces are created through isosurface extraction from volumetric representations, obtained by 3D photography, CT, or MRI. Noise inherent in the acquisition process can lead to geometrical and topological errors. Reducing geometrical errors during reconstruction is well studied. However, isosurfaces often contain many topological errors in the form of tiny handles. These nearly invisible artifacts hinder subsequent operations like mesh simplification, remeshing, and parametrization. In this article we present a practical method for removing handles in an isosurface. Our algorithm makes an axis-aligned sweep through the volume to locate handles, compute their sizes, and selectively remove them. The algorithm is designed to facilitate out-of-core execution. It finds the handles by incrementally constructing and analyzing a Reeb graph. The size of a handle is measured by a short non-separating cycle. Handles are removed robustly by modifying the volume rather than attempting “mesh surgery.” Finally, the volumetric modifications are spatially localized to preserve geometrical detail. We demonstrate topology simplification on several complex models, and show its benefits for subsequent surface processing.
	Variational Shape Approximation David Cohen-Steiner, Pierre Alliez, and Mathieu Desbrun ACM Trans. of Graphics (SIGGRAPH '04). Abstract: Achieving efficiency in mesh processing often demands that overly verbose 3D datasets be reduced to more concise, yet faithful representations. Despite numerous applications ranging from geometry compression to reverse engineering, concisely capturing the geometry of a surface remains a tedious task. In this paper, we present both theoretical and practical contributions that result in a novel and versatile framework for geometric approximation of surfaces. We depart from the usual strategy by casting shape approximation as a variational geometric partitioning problem. Using the concept of geometric proxies, we drive the distortion error down through repeated clustering of faces into best-fitting regions. Our approach is entirely discrete and error-driven, and does not require parameterization or local estimations of differential quantities. We also introduce a new metric based on normal deviation, and demonstrate its superior behavior at capturing anisotropy.
	Discrete Exterior Calculus for Variational Problems in Computer Graphics and Vision Mathieu Desbrun, Anil Hirani, and Jerrold E. Marsden In the 42nd IEEE Conference on Decision and Control Proceedings (CDC '03), 42, 4902-4907. Abstract: This paper demonstrates how discrete exterior calculus tools may be useful in computer vision and graphics. A variational approach provides a link with mechanics. [This is an invited paper, gathering different pieces of work already published]
	Interactive Extraction of High-Frequency Aesthetically-Coherent Colormaps Santiago V. Lombeyda and Mathieu Desbrun Technical report, Caltech, 2003. Abstract: Color transfer functions (i.e. colormaps) exhibiting a high frequency luminosity component have proven to be useful in the visualization of data where feature detection or iso-contours recognition is essential. Having these colormaps also display a wide range of color and an aesthetically pleasing composition holds the potential to further aid image understanding and analysis. However producing such colormaps in an efficient manner with current colormap creation tools is difficult. We hereby demonstrate an interactive technique for extracting colormaps from artwork and pictures. We show how the rich and careful color design and dynamic luminance range of an existing image can be gracefully captured in a colormap and be utilized effectively in the exploration of complex datasets.
	Discrete Shells Eitan Grinspun, Anil Hirani, Mathieu Desbrun and Peter Schröder In ACM/Eurographics Symposium of Computer Animation 2003 Abstract: In this paper we introduce a discrete shell model describing the behavior of thin flexible structures, such as hats, leaves, and aluminum cans, which are characterized by a curved undeformed configuration. Previously such models required complex continuum mechanics formulations and correspondingly complex algorithms. We show that a simple shell model can be derived geometrically for triangle meshes and implemented quickly by modifying a standard cloth simulator. Our technique convincingly simulates a variety of curved objects with materials ranging from paper to metal, as we demonstrate with several examples including a comparison of a real and simulated falling hat. Check out the videos on the Multires Group website
	Learning Controls for Blend Shape Based Realistic Facial Animation Pushkar Joshi, Wen Tien, Mathieu Desbrun and Fred Pighin In ACM/Eurographics Symposium of Computer Animation 2003 Abstract: Blend shape animation is the method of choice for keyframe facial animation: a set of blend shapes (key facial expressions) are used to define a linear space of facial expressions. However, in order to capture a significant range of complexity of human expressions, blend shapes need to be segmented into smaller regions where key idiosyncracies of the face being animated are present. Performing this segmentation by hand requires skill and a lot of time. In this paper, we propose an automatic, physically-motivated segmentation that learns the controls and parameters directly from the set of blend shapes. We show the usefulness and efficiency of this technique for both, motion-capture animation and keyframing. We also provide a rendering algorithm to enhance the visual realism of a blend shape model. Movies (divX): Capture, Result, Editing1, Editing2, Editing3.
	Anisotropic Polygonal Remeshing Pierre Alliez, David Cohen-Steiner, Olivier Devillers, Bruno Lévy, and Mathieu Desbrun In ACM SIGGRAPH '03 / ACM TOG Abstract: In this paper, we propose a novel polygonal remeshing technique that exploits a key aspect of surfaces: the intrinsic anisotropy of natural or man-made geometry. In particular, we use curvature directions to drive the remeshing process, mimicking the lines that artists themselves would use when creating 3d models from scratch. After extracting and smoothing the curvature tensor field of an input geometry, lines of minimum and maximum curvatures are used to determine adequate edges for the remeshed version in anisotropic regions, while spherical regions are simply point-sampled since there is no natural direction of symmetry locally. As a result our technique generates polygon meshes mainly composed of quads on anisotropic regions, and of triangles in spherical regions. Our approach provides the flexibility to produce meshes ranging from isotropic to anisotropic, from coarse to dense, and from uniform to curvature adapted.
	Non-iterative, Feature-Preserving Mesh Smoothing Thouis R. Jones, Frédo Durand, and Mathieu Desbrun In ACM SIGGRAPH '03 / ACM TOG Abstract: With the increasing use of geometry scanners to create 3D models, there is a rising need for fast and robust mesh smoothing to remove inevitable noise in the measurements. While most previous work has favored diffusion-based iterative techniques for feature-preserving smoothing, we propose a radically different approach, based on robust statistics and local first-order predictors of the surface. The robustness of our local estimates allows us to derive a non-iterative feature-preserving filtering technique applicable to arbitrary "triangle soups". We demonstrate its simplicity of implementation and its efficiency, which makes it an excellent solution for smoothing large, noisy, and non-manifold meshes.
	Discrete Multiscale Vector Field Decomposition Yiying Tong, Santiago Lombeyda, Anil Hirani, Mathieu Desbrun In ACM SIGGRAPH '03 / ACM TOG Abstract: While 2D and 3D vector fields are ubiquitous in computational sciences, their use in graphics is often limited to regular grids, where computations are easily handled through finite-difference methods. In this paper, we propose a set of simple and accurate tools for the analysis of 3D discrete vector fields on arbitrary tetrahedral grids. We introduce a variational, multiscale decomposition of vector fields into three intuitive components: a divergence-free part, a curl-free part, and a harmonic part. We show how our discrete approach matches its well-known smooth analog, called the Helmotz-Hodge decomposition, and that the resulting computational tools have very intuitive geometric interpretation. We demonstrate the versatility of these tools in a series of applications, ranging from data visualization to fluid and deformable object simulation.
	Progressive Encoding of Complex Isosurfaces (see our executable) Haeyoung Lee, Mathieu Desbrun, and Peter Schröder In ACM SIGGRAPH '03 / ACM TOG Abstract: We present a progressive encoding technique specifically designed for complex isosurfaces. It achieves better rate distortion performance than all standard mesh coders, and even improves on all previous single rate isosurface coders. Our novel algorithm handles isosurfaces with or without sharp features, and deals gracefully with high topologic and geometric complexity. The inside/outside function of the volume data is progressively transmitted through the use of an adaptive octree, while a local frame based encoding is used for the fine level placement of surface samples. Local patterns in topology and local smoothness in geometry are exploited by context-based arithmetic encoding, allowing us to achieve an average of 6.3 bits per vertex (b/v) at very low distortion. Of this rate only 0.69 b/v are dedicated to connectivity data: this improves by 18% over the best previous single rate isosurface encoder.
	Haptic Editing for Decoration and Material Properties Laehyun Kim, Gaurav S. Sukhatme and Mathieu Desbrun Accepted in 11th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, IEEE Computer Society, 2003 Abstract: In this paper, we explore haptic editing as a powerful way to enhance haptic realism. Building upon the framework of a previous implicit-based haptic technique, our haptic decoration technique allows the user to first paint directly on 3D models, and then to sense the thickness variation due to the added paint. Meanwhile, material editing permits the user to edit and feel local material properties such as friction and stiffness in a natural way. In addition, we extended the initial haptic model to support some novel features including a magnetic surface attraction that forces the tool tip to stick to the surface of complex models.
	An Implicit-based Haptic Rendering Technique (go to the haptics page to download library) Laehyun Kim, Anna Kyrikou, Gaurav S. Sukhatme and Mathieu Desbrun In IEEE/RSJ IROS 2002 Proceedings Abstract: We present a novel haptic rendering technique. Building upon previous work, we propose a haptic model based on a volumetric description of the geometry of an object. Unlike previous volumetric approaches, we also find a virtual contact point on the surface in order to derive a penalty force that is consistent with the real geometry of the object, without introducing force discontinuity. We also demonstrate that other surface properties such as friction and texture can be added elegantly. The resulting technique is fast (1000 Hz refresh rate) and can handle large geometry models on low-end computers.
	Intrinsic Parameterizations of Surface Meshes (here is a hindsight: LSCM=DNCP) Mathieu Desbrun, Mark Meyer, and Pierre Alliez In Eurographics 2002 Conference Proceedings Abstract: Parameterization of discrete surfaces is a fundamental and widely-used operation in graphics, required, for instance, for texture mapping or remeshing. As 3D data becomes more and more detailed, there is an increased need for fast and robust techniques to automatically compute least-distorted parameterizations of large meshes. In this paper, we present new theoretical and practical results on the parameterization of triangulated surface patches. Given a few desirable properties such as rotation and translation invariance, we show that the only admissible parameterizations form a two-dimensional set and each parameterization in this set can be computed using a simple, sparse, linear system. Since these parameterizations minimize the distortion of different intrinsic measures of the original mesh, we call them Intrinsic Parameterizations. In addition to the theoretical analysis, we propose robust, efficient and tunable tools to obtain least-distorted parameterizations automatically. In particular, we give details on a novel, fast technique to provide an optimal mapping without fixing any boundary conditions, thus providing a unique Natural Intrinsic Parameterization. Other techniques based on this parameterization family, designed to ease the rapid design of parameterizations, are also proposed.
	Processing Irregular Meshes Mathieu Desbrun In Shape Modelling International '02 Conference Proceedings Abstract: Most meshes are usually produced with both topological and geometrical irregularity (arbitrary valence, non-uniform sampling). This has been seen as a flaw hindering subsequent mesh processing, because most of the other signals we manipulate everyday (sound, image, video) are acquired and processed as regularly sampled data. Three-dimensional (3D) signals, be they surfaces or volumes, are however drastically and inherently different. Although the main body of work on mesh processing has focused on semi-regular meshes (on which the usual DSP tools can be extended quite nicely), we have focused on fully irregular meshes. Understanding this problem of irregularity, inherent to 3D sampling, is fundamental in widely different applications ranging from mesh modeling to smoothing, parameterization, remeshing, and to even compression or animation. In this talk, we will show some of our latest results (both theoretical and practical) and will also point to the remaining challenges. [This is just a short overview to illustrate an invited talk]
	Angle-Analyzer: A Triangle-Quad Mesh Codec Haeyoung Lee, Pierre Alliez, and Mathieu Desbrun In Eurographics 2002 Conference Proceedings Abstract: We present Angle-Analyzer, a new single-rate compression algorithm for triangle-quad hybrid meshes. Using a carefully-designed geometry-driven mesh traversal and an efficient encoding of intrinsic mesh properties, Angle-Analyzer produces compression ratios 40\% better in connectivity and 20% better in geometry than the leading Touma and Gotsman technique for the same level of geometric distortion. The simplicity and performance of this new technique is demonstrated, and we provide extensive comparative tests to contrast our results with the current state-of-the-art techniques.
	Interactive Geometry Remeshing Pierre Alliez, Mark Meyer, and Mathieu Desbrun In Siggraph 2002 Conference Proceedings Abstract: We present a novel technique, both flexible and efficient, for interactive remeshing of irregular geometry. First, the original (arbitrary genus) mesh is substituted by a series of 2D maps in parameter space. Using these maps, our algorithm is then able to take advantage of established signal processing and halftoning tools that offer real-time interaction and intricate control. The user can easily combine these maps to create a control map, a map which controls the sampling density over the surface patch. This map is then near-optimally sampled at interactive rates allowing the user to interactively design a tailored resampling. Once this sampling is complete, a Delaunay triangulation and fast optimization are performed to perfect the final mesh. As a result, our remeshing technique is extremely versatile and general being able to produce arbitrarily complex meshes with a variety of properties including: uniformity, regularity, semi-regularity, curvature sensitive resampling, and feature preservation. We provide a high level of control over the sampling distribution allowing the user to interactively custom design the mesh based on their requirements thereby increasing their productivity in creating a large variety of meshes.
	Generalized Barycentric Coordinates for Irregular N-gons Mark Meyer, Haeyoung Lee, Alan H. Barr, Mathieu Desbrun Accepted in Journal of Graphics Tools Abstract: In this paper we develop a generalized form of barycentric coordinates for irregular, convex n-sided polygons. Triangular barycentric coordinates have had many classical applications in computer graphics, from texture mapping to ray-tracing. Our new equations preserve many of the familiar properties of the triangular barycentric coordinates, which suggests that the new n-sided formulation can prove to be similarly useful. We exhibit the properties and behavior of these new generalized barycentric coordinates through several examples of applications.
	Discrete Differential-Geometry Operators for Triangulated 2-Manifolds Mark Meyer, Mathieu Desbrun, Peter Schröder, Alan H. Barr VisMath '02, Berlin (Germany) Abstract: This paper provides a consistent set of flexible tools to approximate important geometric attributes, including normal vectors and curvatures, on arbitrary 2D and 3D meshes embedded in n dimensions. We present a consistent derivation of these first and second order differential properties using Voronoi cells and the mixed Finite Element/Finite Volume method. The new operators are closely related to the continuous case, guaranteeing an appropriate extension from the continuous to the discrete setting: they respect the intrinsic properties of the continuous differential operators. We show that these estimates are optimal in accuracy under mild smoothness condi-tions, and demonstrate their numerical quality. We finally present applications of these operators, such as mesh smoothing and enhancement, quality checking, and denoising of arbitrary vectors fields, such as flow fields or tensor images.
	Near-Optimal Connectivity Encoding of 2-Manifold Polygon Meshes Andrei Khodakovsky, Pierre Alliez, Mathieu Desbrun, and Peter Schröder Graphical Models 64(3-4), pp. 147-168, 2002 Abstract: Encoders for triangle mesh connectivity based on enumeration of vertex valences are among the best reported to date. They are both simple to implement and report the best compressed file sizes for a large corpus of test models. Additionally they have recently been shown to be near-optimal since they realize the Tutte entropy bound for all planar triangulations. In this paper we introduce a connectivity encoding method which extends these ideas to 2-manifold meshes consisting of faces with arbitrary degree. The encoding algorithm exploits duality by applying valence enumeration to both the primal and dual mesh in a symmetric fashion. It generates two sequences of symbols, vertex valences and face degrees, and encodes them separately using two context-based arithmetic coders. This allows us to exploit vertex and/or face regularity if present. When the mesh exhibits perfect face regularity (e.g., a pure triangle or quad mesh) and/or perfect vertex regularity (resp. valence six or four) the corresponding bit rate vanishes to zero asymptotically. For triangle meshes, our technique is equivalent to earlier valence driven approaches. We report compression results for a corpus of standard meshes. In all cases we are able to show coding gains over earlier coders, sometimes as large as 50%. Remarkably, this is true even for coders specialized to triangle or quad meshes. A theoretical analysis re-veals that our approach is near-optimal as we achieve the Tutte en-tropy bound for arbitrary planar graphs of 2 bits per edge in the worst case.
	Interactive Animation of Cloth-like Objects in Virtual Reality. Mark Meyer, Gilles Debunne, Mathieu Desbrun, Alan H. Barr The Journal of Visualization and Computer Animation, Volume 12, Issue 1, May 2001, pages 1-12. Abstract: Modeling and animation of cloth has experienced important developments in recent years. As a consequence, complex textile models can be used to realistically drape objects or human characters in a fairly efficient way. However, real-time realistic simulation remains a major challenge, even if applications are numerous, from rapid prototyping to e-commerce. In this paper, we present a stable, real-time al-gorithm for animating cloth-like materials. Using a hybrid explicit/implicit algorithm, we perform fast and stable time integration of a physically-based model with rapid collision detection and response, as well as wind or liquid drag effects to enhance realism. We demonstrate our approach through a series of examples in VR environments, proving that real-time animation of cloth, even on low-end computers, is now achievable.
	Efficient View-dependent Refinement of 3D Meshes using Sqrt(3)-Subdivision (pdf, A4 format, 3.5 MBytes) Pierre Alliez, Nathalie Laurent, Henri Sanson and Francis Schmitt In Visual Computer Abstract: In this paper we introduce an efficient view dependent refinement technique well-suited to adaptive visualization of 3D triangle meshes on a graphic terminal. Our main goal is the design of fast and robust smooth surface reconstruction from coarse meshes. We demonstrate that the sqrt{3} subdivision operator recently introduced by Kobbelt offers many benefits, including view-dependent refinement, removal of polygonal aspect and highly tunable level of detail adaptation. In particular, we propose a new data structure that requires neither edges nor hierarchies for efficient and reversible view-dependent refinement. Results on various 3D meshes illustrate the relevance of the technique.
	Valence-Driven Connectivity Encoding for 3D Meshes [Slides, 8 MBytes] Pierre Alliez and Mathieu Desbrun In EUROGRAPHICS '2001 Conference Proceedings Abstract: In this paper, we propose a valence-driven, single-resolution encoding technique for lossless compression of triangle mesh connectivity. Building upon a valence-based approach pioneered by Touma and Gotsman, we design a new valence-driven conquest for arbitrary meshes that always guarantees smaller compression rates than the original method. Furthermore, we provide a novel theoretical entropy study of our technique, hinting the optimality of the valence-driven approach. Finally, we demonstrate the practical efficiency of this approach (in agreement with the theoretical prediction) on a series of test meshes, resulting in the lowest compression ratios published so far, for both irregular and regular meshes, small or large.
	Meshes on Fire Haeyoung Lee, Laehyun Kim, Mark Meyer, Mathieu Desbrun In EG Workshop on Computer Animation and Simulation '2001 Abstract:We present a new method for the animation of fire on polyhedral surfaces. Using the notion of discrete straightest geodesics, we evolve fire fronts directly on the surface of arbitrarily complex objects. Animator control and motion complexity is achieved by driving the fire motion using multi-scale turbulent wind fields and geometric quantities. Our model also supports adaptivity of the fire fronts, multiple simultaneous fires, and merging of multiple fires. This new technique produces convincing simulations at interactive rates even on a low-end PC, greatly increasing the productivity of the animation design process.
	Dynamic Real-Time Deformations using Space and Time Adaptive Sampling Gilles Debunne, Mathieu Desbrun, Alan H. Barr and Marie-Paule Cani In ACM SIGGRAPH '01 Conference Proceedings Abstract: This paper presents a robust, adaptive method for animating dynamic visco-elastic deformable objects that provides a guaranteed frame rate. Our approach uses a novel automatic space and time adaptive level of detail technique, in combination with a large-displacement (Green) strain tensor formulation. The body is partitioned in a non-nested multiresolution hierarchy of tetrahedral meshes. The local resolution is determined by a quality condition that indicates where and when the resolution is too coarse. As the object moves and deforms, the sampling is refined to concentrate the computational load into the regions that deform the most. Our model consists of a continuous differential equation that is solved using a local explicit finite element method. We demonstrate that our adaptive Green strain tensor formulation suppresses unwanted artifacts in the dynamic behavior, compared to adaptive mass-spring and other adaptive approaches. In particular, damped elastic vibration modes are shown to be nearly unchanged for several levels of refinement. Results are presented in the context of a virtual reality system. The user interacts in real-time with the dynamic object through the control of a rigid tool, attached to a haptic device driven with forces derived from the method.
	Progressive Encoding for Lossless Transmission of 3D Meshes - (1200 dpi,9.8 MBytes) [300 dpi, 2.4 MBytes] [Slides, 8 MBytes] Pierre Alliez and Mathieu Desbrun In ACM SIGGRAPH '01 Conference Proceedings Abstract: Lossless transmission of 3D meshes is a very challenging and timely problem for many applications, ranging from collaborative design to engineering. Additionally, frequent delays in transmissions call for progressive transmission in order for the end user to receive useful successive refinements of the final mesh. In this paper, we present a novel, fully progressive encoding approach for lossless transmission of triangle meshes with a very fine granularity. A new valence-driven decimating conquest, combined with patch tiling and an original strategic retriangulation is used to maintain the regularity of valence. We demonstrate that this technique leads to good mesh quality, near-optimal connectivity encoding, and therefore a good rate-distortion ratio throughout the transmission. We also improve upon previous lossless geometry encoding by decorrelating the normal and tangential components of the surface. For typical meshes, our method compresses connectivity down to less than 3.7 bits per vertex, 40% better in average than the best methods previously reported; we further reduce the usual geometry bit rates by 20% in average by exploiting the smoothness of meshes. Concretely, our technique can reduce an ascii VRML 3D model down to 1.7% of its size for a 10-bit quantization (2.3% for a 12-bit quantization) while providing a very progressive reconstruction.
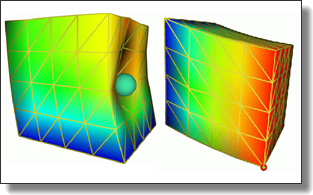	Adaptive Simulation of Soft Bodies in Real-Time Gilles Debunne, Mathieu Desbrun, Marie-Paule Cani, Alan H. Barr In Computer Animation '00 Abstract: This paper presents an adaptive technique to animate deformable bodies in real-time. In contrast to most previous work, we introduce a multi-resolution model that locally refines or simplifies the simulated object over time in order to optimize the computational effort. We use the mixed Finite-Volume/Finite-Element method to derive fast, local discrete differential operators over irregular grids with tight error bounds. The linear elasticity equations can be simulated using an arbitrary non-nested hierarchy of volumetric meshes, allowing the computation load to be automatically concentrated where and when needed. Real-time simulation, with a guaranteed frame rate, can be achieved as demonstrated through a series of examples on our video.
	Semi-Regular Mesh Extraction from Volumes Zoë J. Wood, Mathieu Desbrun, Peter Schröder, David Breen In ACM/IEEE Visualization '00 Proceedings Abstract: We present a novel method to extract iso-surfaces from distance volumes. It generates high quality semi-regular multiresolution meshes of arbitrary topology. Our technique proceeds in two stages. First, a very coarse mesh with guaranteed topology is extracted. Subsequently an iterative multi-scale force-based solver refines the initial mesh into a semi-regular mesh with geometrically adaptive sampling rate and good aspect ratio triangles. The coarse mesh extraction is performed using a new approach we call surface wave-front propagation. A set of discrete iso-distance ribbons are rapidly built and connected while respecting the topology of the iso-surface implied by the data. Subsequent multi-scale refinement is driven by a simple force-based solver designed to combine good iso-surface fit and high quality sampling through reparameterization. In contrast to the Marching Cubes technique our output meshes adapt gracefully to the iso-surface geometry, have a natural multiresolution structure and good aspect ratio triangles, as demonstrated with a number of examples.
	Anisotropic Feature-Preserving Denoising of Bivariate Data Mathieu Desbrun, Mark Meyer, Peter Schröder, Alan H. Barr In Graphics Interface '00 Proceedings Abstract: In this paper, we present an efficient way to denoise bivariate data like height fields, color pictures or vector fields, while preserving edges and other features. Mixing surface area minimization, graph flow, and nonlinear edge preservation metrics, our method generalizes previous anisotropic diffusion approaches in image processing, and is applicable to data of arbitrary dimension. Another notable difference is the use of a more robust discrete differential operator, which captures the fundamental surface properties. We demonstrate the method on range images and height fields, as well as greyscale or color images.
	Implicit Fairing of Arbitrary Meshes using Diffusion and Curvature Flow Mathieu Desbrun, Mark Meyer, Peter Schröder, Alan H. Barr In ACM Siggraph '99 Proceedings Abstract: In this paper, we develop methods to rapidly remove rough features from irregularly triangulated data intended to portray a smooth surface. The main task is to remove undesirable noise and uneven edges while retaining desirable geometric features. The problem arises mainly when creating high-fidelity computer graphics objects using imperfectly-measured data from the real world. Our approach contains three novel features: an implicit integration method to achieve efficiency, stability, and large time-steps; a scale-dependent Laplacian operator to improve the diffusion process; and finally, a robust curvature flow operator that achieves a smoothing of the shape itself, distinct from any parameterization. Additional features of the algorithm include automatic exact volume preservation, and hard and soft constraints on the positions of the points in the mesh. We compare our method to previous operators and related algorithms, and prove that our curvature and Laplacian operators have several mathematically-desirable qualities that improve the appearance of the resulting surface. In consequence, the user can easily select the appropriate operator according to the desired type of fairing. Finally, we provide a series of examples to graphically and numerically demonstrate the quality of our results.
	Interactive multiresolution animation of deformable models Gilles Debunne, Mathieu Desbrun, Alan Barr, and Marie-Paule Cani In Eurographics Workshop on Computer Animation and Simulation '99 Abstract: This paper presents an approach to animate elastic deformable materials at interactive rates using space-time adaptive resolution. We propose a new computational model, based on the conventional Hooke’s law, that uses a discrete approximation of differential operators on irregular grid. It allows local refinement or simplification of the computational model based on local error measurement. We in effect minimize calculations while ensuring a realistic and scale-independent behavior within a given accuracy threshold. We demonstrate this technique on a real-time virtual liver surgery application.
	Interactive Animation of Structured Deformable Objects  Mathieu Desbrun, Peter Schröder, Alan H. Barr In Graphics Interface '99 Abstract: In this paper, we propose a stable and efficient algorithm for animating mass-spring systems. An integration scheme derived from implicit integration allows us to obtain interactive realistic animation of any mass-spring network. We alleviate the need to solve a linear system through the use of a predictor-corrector approach: We first compute a rapid approximation of the implicit integration, then we correct this estimate in a post-step process to preserve momentum. Combined with an inverse kinematics process to implement collisions and other constraints, this method provides a simple, stable and tunable model for deformable objects suitable for virtual reality. An implementation in a VR environment demonstrates this approach.
	Active Implicit Surface for Animation Mathieu Desbrun and Marie-Paule Cani-Gascuel In Graphics Interface'98 Abstract:This paper introduces a new model of deformable surfaces designed for animation, which we call active implicit surfaces. The underlying idea is to animate a potential field defined by discrete values stored in a grid, rather than directly animating a surface. This surface, defined as an iso-potential of the field, has the ability to follow a given object using a snake-like strategy. Surface tension and other characteristics such as constant surface area or constant volume may be added to this model. The implicit formulation allows the surface to easily experience topology changes during simulation. We present an optimized implementation: computations are restricted to a close neighborhood around the surface. Applications range from the coating of deformable materials simulated by particle systems (the surface hides the granularity of the underlying model) to the generation of metamorphosis between shapes that may not have the same topology.
	Space-Time Adaptive Simulation of Highly Deformable Substances Mathieu Desbrun, Marie-Paule Cani INRIA Technical Report, '98 Abstract: This report presents an approach for efficiently, yet precisely simulating highly deformable substances ranging from solids to liquids. The key idea is to use a state equation for specifying the dynamics of the substance. During a simulation, the material is sampled by particles that derive their interaction forces from this state equation. Since this ensures the same qualitative behavior whatever the discretization rate, an adaptive scheme can be used during simulations: the particle system adapts over space and time according to a given compromise between precision and computational efficiency. The system refines (i.e., particles are subdivided) in areas undergoing large or fast deformations, while it simplifies (i.e., neighboring particles are merged) in stable regions. Meanwhile, the values of the individual integration time steps used for each particle are automatically adapted to avoid instabilities. An active implicit surface is used to visualize the substance. It smoothly coats the particles and filters internal changes of granularity over time..
	Animation of Deformable Models using Implicit Surfaces Marie-Paule Cani-Gascuel and Mathieu Desbrun IEEE Transactions on Vision and Computer Graphics, March 97 Abstract: This paper presents a general approach for designing and animating complex deformable models with implicit surfaces. Implicit surfaces are introduced as an extra layer coating any kind of structure that moves and deforms over time. O ering a compact de nition of a smooth surface around an object, they provide an efficient collision detection mechanism. The implicit layer deforms in order to generate exact contact surfaces between colliding bodies. A simple physically-based model approximating elastic behavior is then used for computing collision response. The implicit formulation also eases the control of the object's volume with a new method based on local controllers. We present two different applications that illustrate the benefits of these techniques. First, the animation of simple characters made of articulated skeletons coated with implicit flesh exploits the compactness and enhanced control of the model. The second builds on the specific properties of implicit surfaces for modeling soft inelastic substances capable of separation and fusion that maintain a constant volume when animated.
	Adaptive Sampling of Implicit Surfaces for Interactive Modeling & Animation Mathieu Desbrun, Nicolas Tsingos and Marie-Paule Gascuel in Computer Graphics Forum, 15(5), Dec. 96 Abstract: This paper presents a new adaptive sampling method for implicit surfaces that can been used in both interactive modeling and animation. The algorithm samples implicit objects generated by skeletons and efficiently maintains this sampling, even when their topology changes over time such as during fractures and fusions. It provides two complementary modes of immediate visualization: displaying "scales" lying on the surface, or a piecewise polygonization. The sampling method is particularly well suited to efficiently avoid "unwanted blending" between different parts of an object. Moreover, it can be used for partitioning the implicit surface into local bounding boxes that will accelerate collision detection during animations and ray-intersections during final rendering.
	Smoothed Particles: A new paradigm for highly deformable bodies  Mathieu Desbrun and Marie-Paule Gascuel In 6th Eurographics Workshop on Animation and Simulation'96 Abstract: This paper presents a new adaptive sampling method for implicit surfaces that can been used in both interactive modeling and animation. The algorithm samples implicit objects generated by skeletons and efficiently maintains this sampling, even when their topology changes over time such as during fractures and fusions. It provides two complementary modes of immediate visualization: displaying \scales" lying on the surface, or a piecewise polygonization. The sampling method is particularly well suited to efficiently avoid "unwanted blending" between different parts of an object. Moreover, it can be used for partitioning the implicit surface into local bounding boxes that will accelerate collision detection during animations and ray-intersections during final rendering.
	Animating Soft Substances with Implicit Surfaces Mathieu Desbrun and Marie-Paule Gascuel.  In SIGGRAPH'95 Proceedings Abstract: This paper presents a hybrid model for animation of soft inelastic substance which undergo topological changes, e.g. separation and fusion and which fit with the objects they are in contact with. The model uses a particle system coated with a smooth iso-surface that is used for performing collision detection, precise contact modeling and integration of response forces. The animation technique solves three problems inherent in implicit modeling. Firstly, local volume controllers are defined to insure constant volume deformation, even during highly inelastic processes such as splitting or fusion. Secondly, we avoid unwanted distance blending between disconnected pieces of the same substance. Finally, we simulate both collisions and progressive merging under compression between implicit surfaces that do not blend together. Parameter tuning is facilitated by the layered model and animation is generated at interactive rates.

Last change: Aug 10th, 2020

Under eternal construction. No trees have been injured in the making of this page.

© desbrun / Applied Geometry / Caltech 2004-2020